펜윅 트리(Fenwick Tree)

개요

구간 합(range sum)은 부분 합(partial sum)을 이용하여 아주 빠르게 계산할 수 있다.

• 부분 합: psum[pos] = arr[0] + arr[1] + … + arr[pos]
• [left, right]의 구간 합: psum[right] - psum[left-1]

펜윅 트리(Fenwick Tree) 또는 이진 인덱스 트리(binary indexed tree, BIT)라고 불리는 자료구조는 부분 합을 $O( \log n)$에 빠르게 계산하고, 중간에 배열의 원소의 값이 변경되어도 업데이트를 $O( \log n)$에 수행할 수 있다.

비슷한 아이디어로 세그먼트 트리가 있다. 펜윅 트리는 세그먼트 트리보다 더 적은 메모리를 사용하고, 구현도 간단하다.
하지만 모든 세그먼트 트리 문제를 펜윅 트리로 대체해서 풀 수는 없다. 구간 최댓값, 최솟값 등의 문제는 1개의 펜윅트리만으로는 풀 수 없다. 펜윅 트리는 특히 구간 합에 대해서 최적화된 자료구조라고 생각하면 된다.

펜윅 트리를 이해하기 위해서는 수식의 증명보다, 규칙성을 찾아 일반화를 시키는 게 더 쉽다.
아래 설명부터는 수식보다는 예시를 이용하여 규칙성을 찾고, 바로 일반화를 시킬 것이다. (자세한 증명과 다양한 예시는 각자에게 맡긴다.)

사전지식(C, C++ 코딩)

사전지식1 정수 n을 2진수로 표현 했을 때, 1이 존재하는 최하위 비트 삭제하기.(0으로 만들기)
예를 들어, 1011에 반복 적용하면 1010, 1000, 0000 이 된다.

n &= (n-1)

사전지식2 정수 n을 2진수로 표현 했을 때, 1이 존재하는 최하위 비트에 1을 더하기
예를 들어, 1011에 반복 적용하면 1100, 10000, 100000 이 된다.

n += (n & -n)

기본 구조

구간 합을 구해야 하는 원본 배열 arr이 있고, index 1부터 n까지 데이터가 저장되어 있다고하자.
또한 트리를 저장하기 위해 배열 tree를 선언하자. 이때 tree 배열은 인덱스 1부터 n까지 사용할 것이므로, 사이즈는 n+1이면 된다.

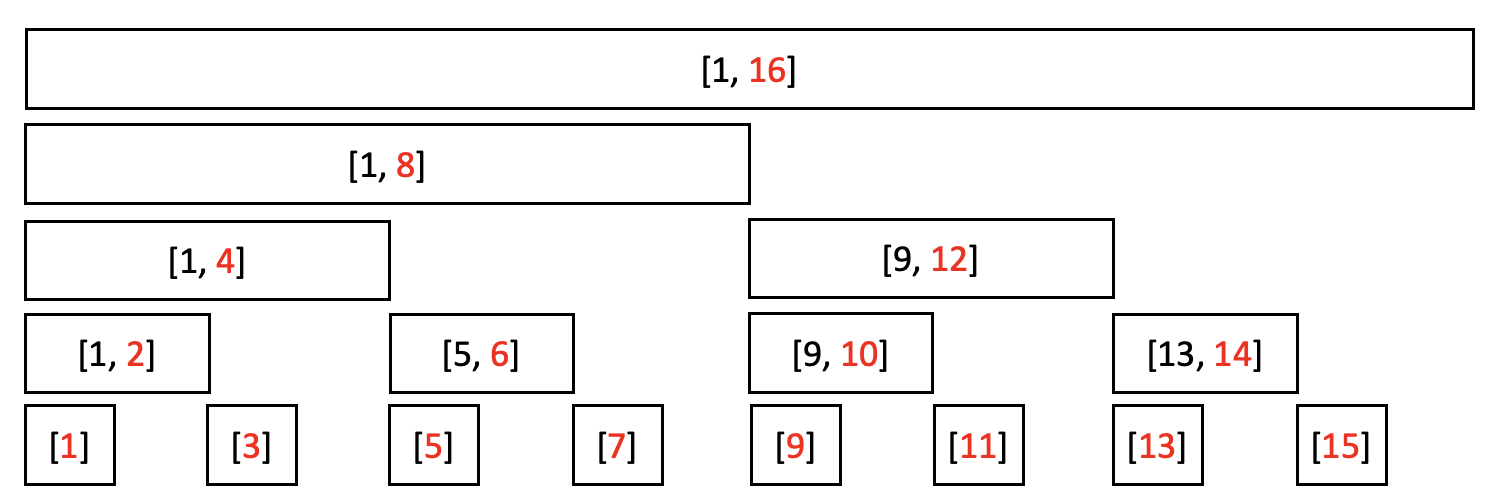
위 이미지에서 빨간색 숫자는 tree[]의 인덱스이고, 각 네모 박스의 구간은 해당 인덱스가 담고 있는 구간 합이다.
이때 구간의 오른쪽 끝은 tree[]의 인덱스와 같다. 예를 들어, tree[8]=arr[1]+arr[2]+...+arr[8] 이고, tree[10]=arr[9]+arr[10]이다.

인덱스와 각 구간은 어떤 관계가 있는지 살펴보자.
예를 들어 tree[12]는 인덱스 = 12, 구간 = [9, 12]이다.
12를 비트로 나타내면 1100이다. 이때 1이 존재하는 최하위 비트가 의미하는 십진수는 $2^2 = 4$이다.
여기서 나온 4가 구간의 길이가 된다.(구간 [9, 12])

한 가지 예시를 더 보자.
10진수 6을 비트로 나타내면 110이다.
1이 존재하는 최하위 비트가 의미하는 십진수는 $2^1=2$이다.
따라서 tree[6]의 구간 길이는 2가 된다.

일반화

십진수 n을 2진수로 표현했을 때, 1이 존재하는 최하위 비트가 의미하는 십진수를 i라 하면
tree[n] = arr[n-i+1] + arr[n-i+2] + … + arr[n]

부분 합 구하기

arr[0] + arr[1] + ... + arr[7]을 구한다고 가정하자.
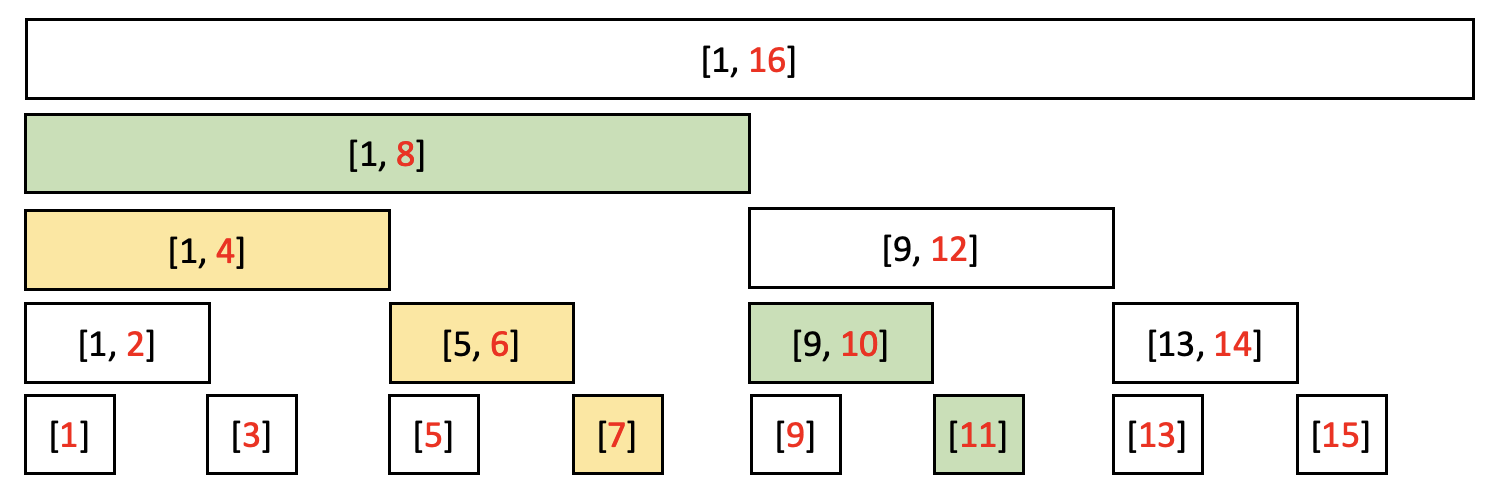
tree[7] + tree[6] + tree[4]를 구해야 한다. (노란색으로 색칠)
이들이 어떤 관계가 있는지 살펴보자.
7은 비트로 111, 6은 비트로 110, 4는 비트로 100이다.
가장 높은 수(7)를 시작으로, 해당 숫자에서 1이 존재하는 최하위 비트를 0으로 바꾸면 된다.
즉, 111 -> 110 -> 100 순서이다.

다른 예로 1부터 11까지의 부분 합을 구해보자.
tree[11] + tree[10] + tree[8]을 구해야 한다.(녹색으로 색칠)
11은 비트로 1011, 10은 비트로 1010, 8은 비트로 1000이다.
위의 경우와 마찬가지로 1이 존재하는 최하위 비트를 0으로 바꾸면 다음 수가 된다.
즉, 1011 -> 1010 -> 1000 순서이다.

코드로 표현하면 다음과 같다.

int sum(int pos) {
  // arr[1] + arr[2] + ... + arr[pos]
  long long ret = 0;
  while (pos > 0) {
      ret += tree[pos];
      pos &= (pos - 1); // 사전지식1
  }
  return ret;
}

원소 업데이트

arr[3]에 $k$를 더하는 연산을 수행한다 가정하자.
arr[3]의 값이 바뀜으로써 영향을 받는 tree[] 원소는 아래 색칠된 것과 같다. (즉, 구간 내에 3이 포함되어 있는 경우이다.)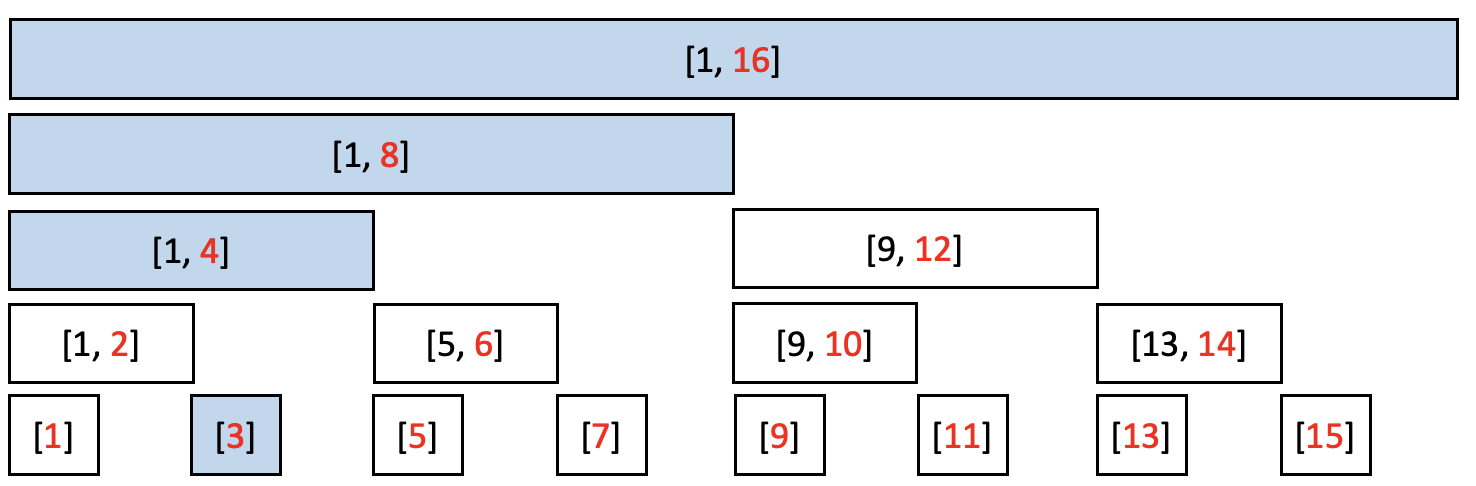

업데이트가 필요한 tree 원소들의 인덱스(3, 4, 8, 16)가 어떤 관계가 있는지 살펴보자.

각 수를 비트로 표현하면 3은 00011, 4는 00100, 8은 01000, 16은 10000이다.
가장 작은 수(3)를 시작으로, 1이 존재하는 최하위 비트에 1을 더하면 다음 수가 나온다.
즉, 00011 -> 00100 -> 01000 -> 10000 순서이다.

코드로 표현하면 다음과 같다.

void update(int pos, long long val) {
    // arr[pos] += val을 수행했을 때
    while (pos <= n) {
        tree[pos] += val;
        pos += (pos & -pos); // 사전지식2
    }
}

문제 예시

https://www.acmicpc.net/problem/2042

이 문제는 모든 펜윅 트리 문제가 그러하듯, 세그먼트 트리로 충분히 풀 수 있다.
하지만 펜윅 트리를 이용하면 수행 시간과 메모리 사용량을 줄일 수 있다.

#include <iostream>
using namespace std;
using ll = long long;

ll arr[1000001], tree[1000001], n;

ll sum(int pos) {
  ll ret = 0;
  while (pos > 0) {
    ret += tree[pos];
    pos &= (pos - 1);
  }
  return ret;
}

void update(int pos, ll val) {
  while (pos <= n) {
    tree[pos] += val;
    pos += (pos & -pos);
  }
}

int main() {
  ll a, b, c, m, k;
  cin >> n >> m >> k;
  for (int i = 1; i <= n; ++i) {
    cin >> arr[i];
    update(i, arr[i]);
  }
  for (int i = 0; i < m + k; ++i) {
    cin >> a >> b >> c;
    if (a == 1) {
        update(b, c - arr[b]);
        arr[b] = c;
    }
    else cout << sum(c) - sum(b - 1) << "\n";
  }
}