Post

Symmetric key Cryptography

Posted Updated
By I Think So 8 min read

Classical Systems

  • Transposition(전치법)
    • 단순히 메시지에 있는 문자의 위치 변경
    • Scytale : 일정 굵기의 봉에 종이를 둘러야 메시지를 읽을 수 있음. key=봉의 굵기
  • Monoalphabetic substitution(단일 문자 치환)
    • Caesar cipher: 알파벳별로 일정한 거리만큼 밀어서 다른 알파벳으로 치환. key=알파벳이 이동한 거리
    • Keyphrase 이용하여 알파벳 대칭표 만들기
      • 예시 : ‘ASSASSINATOR’라는 키워드의 대칭표
      • 키워드에서 중복된 알파벳을 제거 → ASINTOR
      • 이 단어를 앞에 놓고(➊)
      • ASINTOR의 마지막 알파벳인 R부터 Z까지를 뒤에 배치
        • 단, 앞에 나온 알파벳은 제외(➋)
      • 다시 A부터 시작해 중복된 알파벳을 제외하고 배치(➌)

    • Easily broken!
      • Frequency analysis
      • 문자 e와 t가 많이 등장한다는 점, 특정 단어(in, the 등)이 쌍으로 자주 등장한다는 점, 메시지의 내용을 짐작 등
      • 여러 정보를 이용하면 쉽게 깨질 수 있다.
  • Polygram substitution
    • 하나의 문자아 여러 개의 다른 문자로 치환될 수 있음
    • 다중 치환을 이용하여 문자의 발생빈도 균일화
    • Vigenère cipher


Block Cipher

  • 평문과 암호문이 고정된 크기의 블럭으로 구성
  • 다음 블록을 암호화할 때 이전 블록의 결과를 이용 → 원문 블록이 똑같더라도 블록마다 암호문 결과가 다를 수 있음
  • 종류: CBC(Cipher Block Chaining), ECB(Electronic CodeBook), CFB(Cipher FeedBack), OFB(Output FeedBack)

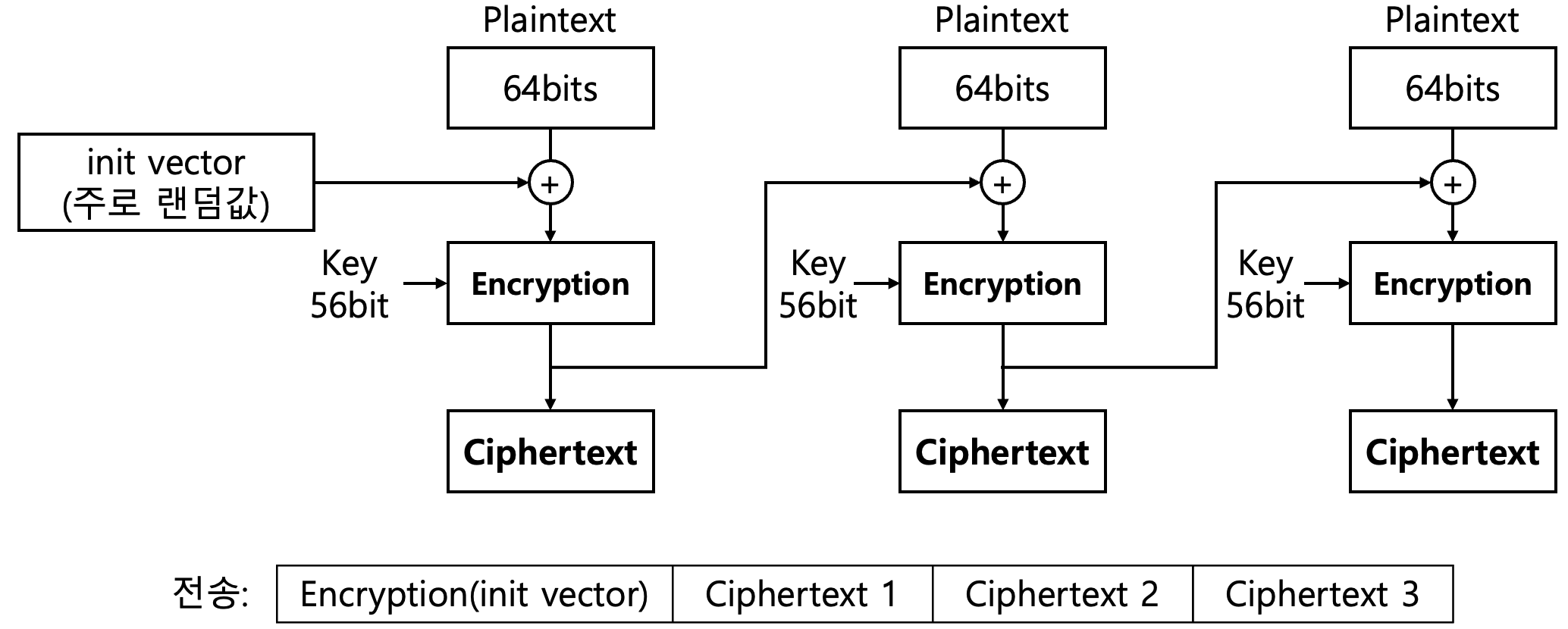
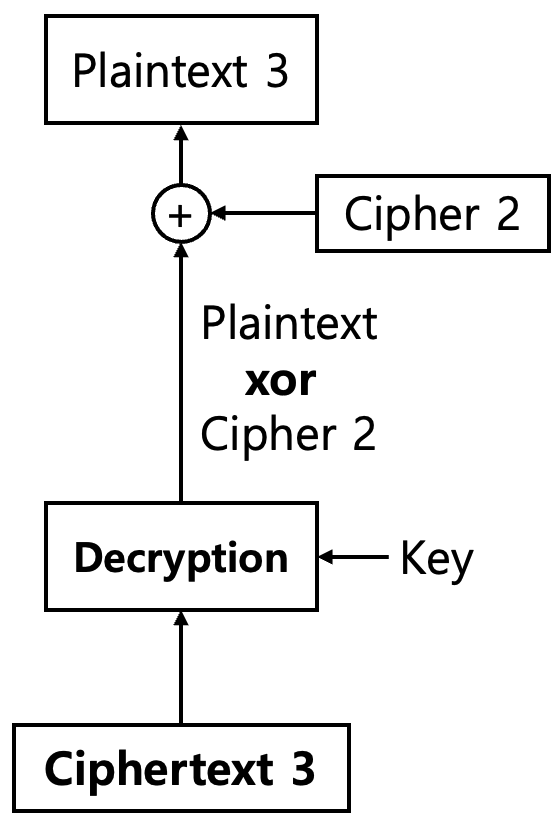
CBC(Cipher Block Chaining)

  • 예시) Block size = 64 bits, key size = 56 bits

Encryption

Decryption. xor의 특성 이용

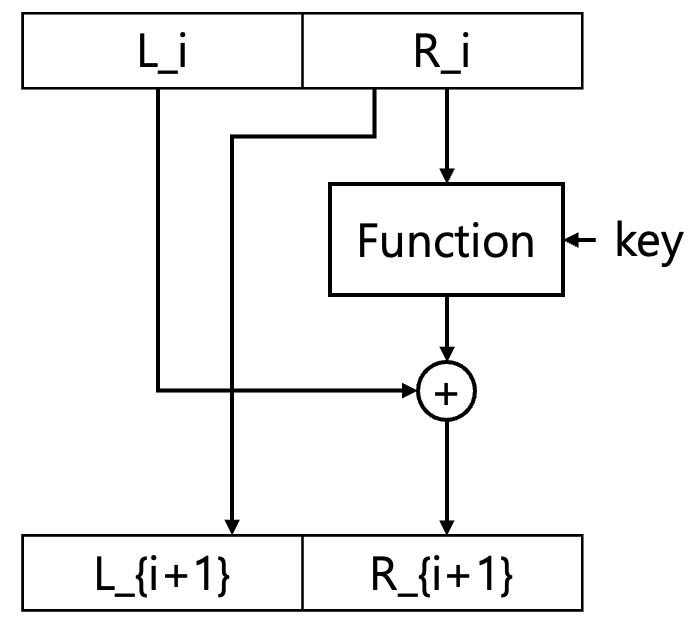
Feistel cipher

  • 블록 암호 설계의 한 형태
  • 암호화 방식이 특정 계산 함수의 반복으로 이루어짐
    • 이때 각 과정에서 사용되는 함수를 ‘round function’이라고 부름
  • 평문을 좌우 반쪽으로 나눔: 평문 = $(L_0,R_0)$
  • 각 회전 $i=1, 2, …, n$ 에서 다음을 계산
    • $L_i= R_{i−1}$
    • $R_i= L_{i−1} \oplus F(R_{i−1},K_i)$
    • 여기서, $F$: 회전 함수, $K_i$: 키
  • 암호문 = $(L_n, R_n)$


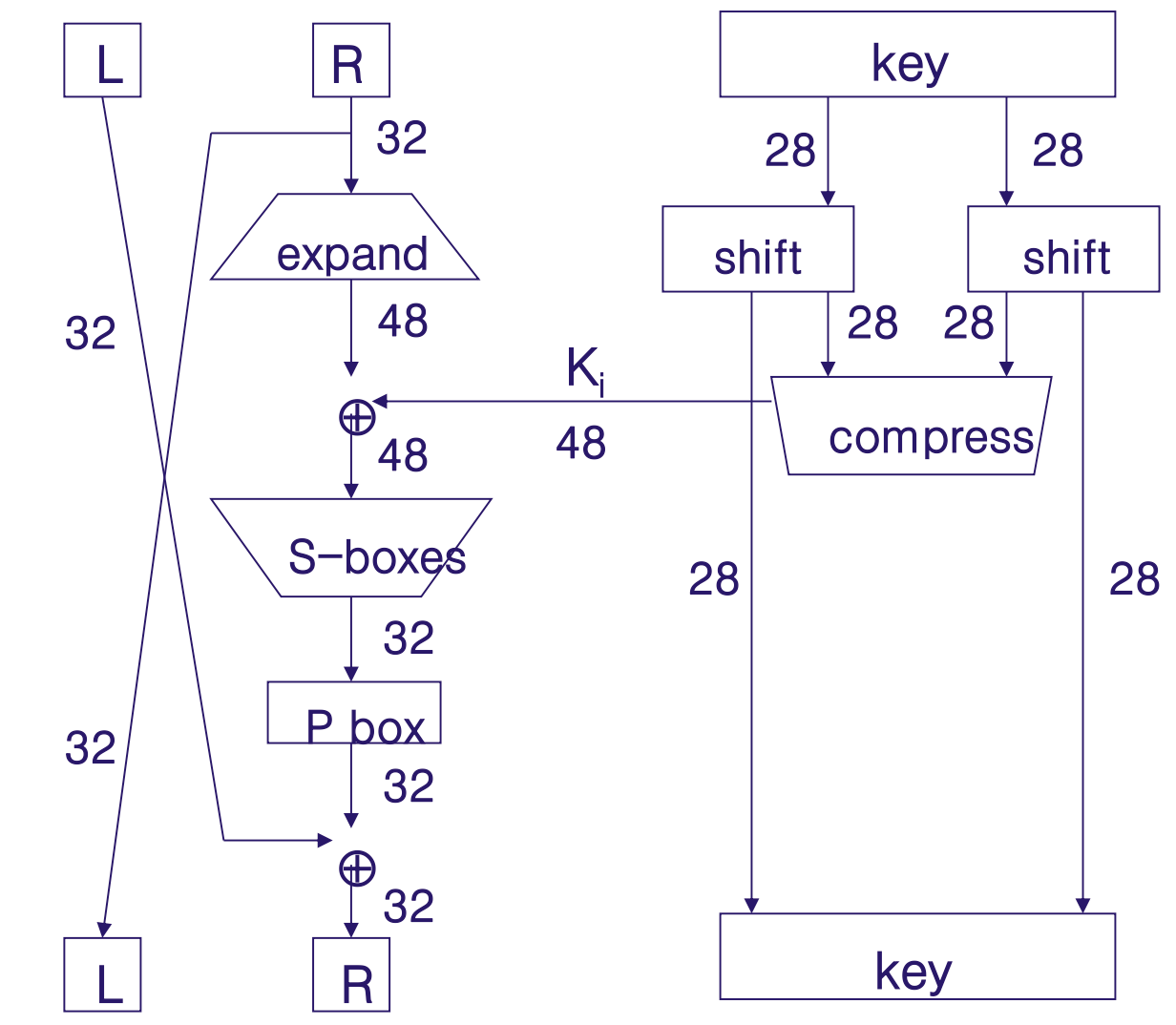
DES(Data Encryption Standard)

  • 64비트의 블록 암호화 알고리즘
  • 16 Round Feistel cipher
  • Key size = 56 bits
  • S-Box(Substitution box), P-Box(Permutation box) 이용
  • 현재는 취약점이 발견되어 사용하지 않음

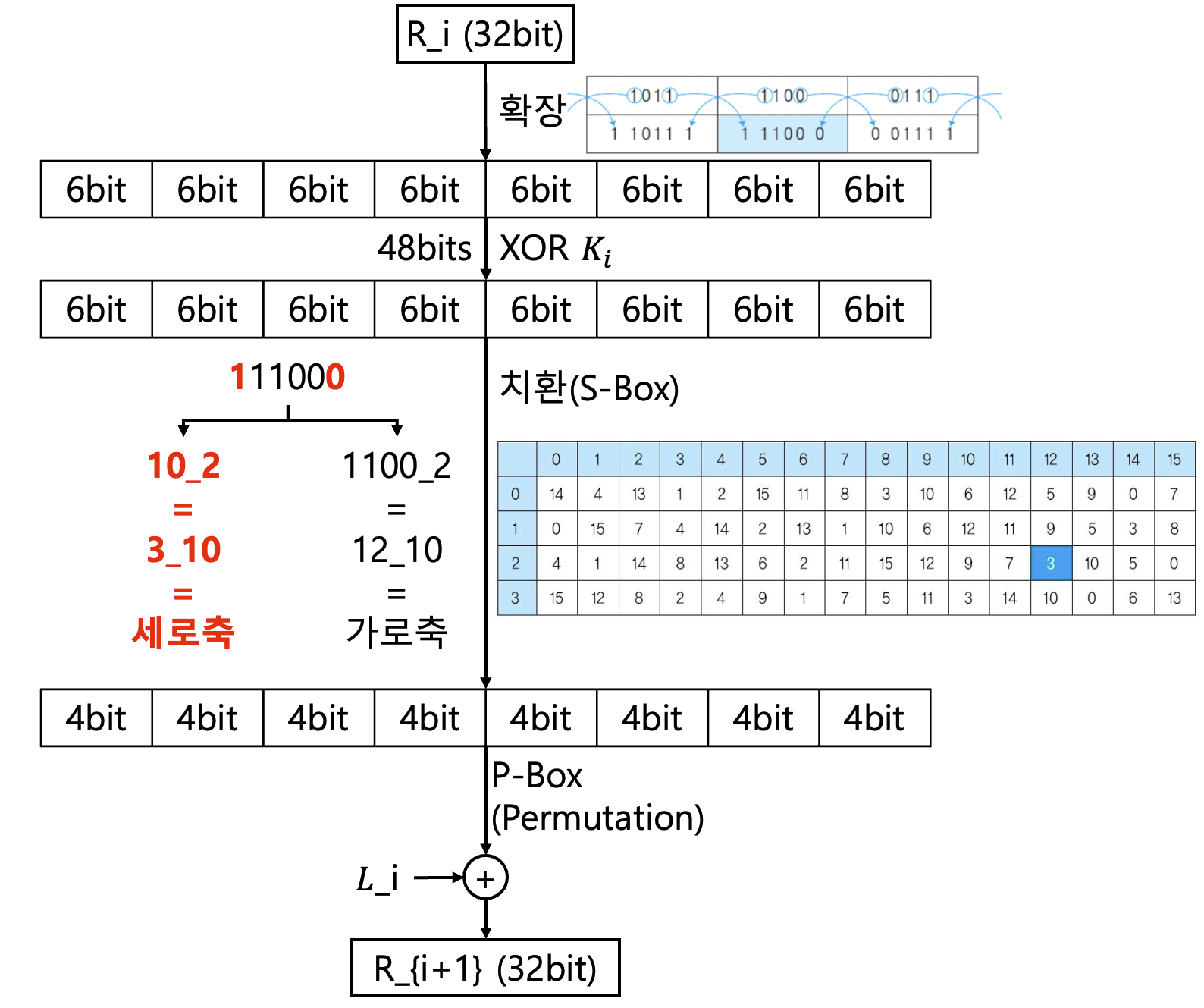
Encryption

  • DES의 56bit key를 적절히 변환시켜서 48bit round key를 생성한다. 실제 XOR을 할 땐 48bit round key를 사용한다.

Detail


Triple DES(3DES)

  • 2개의 key를 이용 (56bit 2개 = 112비트 키를 사용하는 효과)
  • DES는 암호화, 복호화 과정이 서로 역순 과정임을 이용
  • 아래의 E, D는 모두 DES를 이용
  • 암호화: C = E( D( E(P, K1), K2), K1)
    • C1 = E(P, K1)
    • C2 = D(C1, K2)
    • C3 = E(C2, K1)
  • 복호화: P = D( E( D(C,K1), K2), K1)
    • C2 = D(C3, K1)
    • C1 = E(C2, K2)
    • P = D(C1, K1)

왜 Double DES는 없는가?

  • 왜 ‘C=D(E(P, K1),K2)’는 사용하지 않는가?
    • ‘C=E(E(P, K1),K2)’ 등도 모두 마찬가지
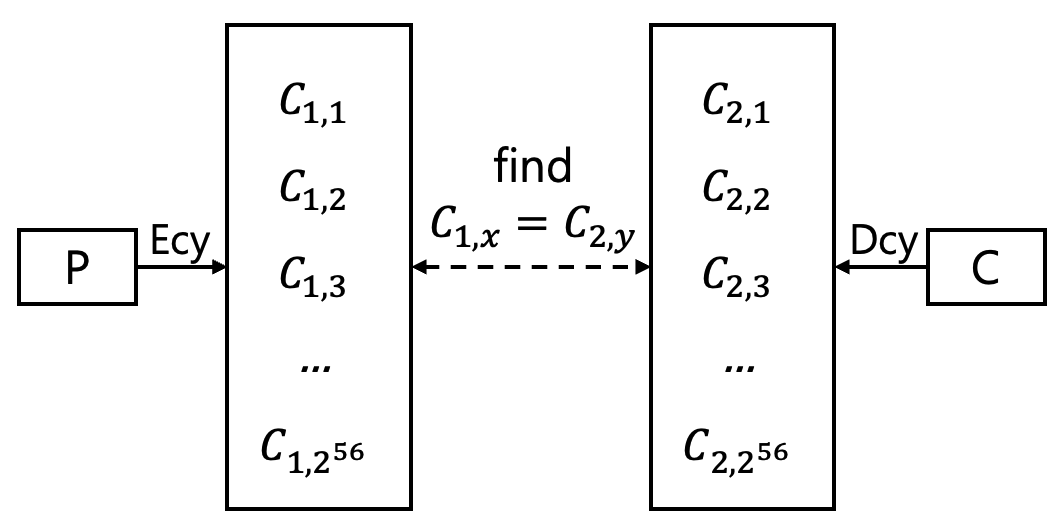
  • 가정: 공격자가 평문 P와 암호문 C의 쌍을 1개 알고있다.
  • 안전성 평가: 공격자는 key를 알아내기 위해 얼마나 많은 시간이 소요되는가?
  • key를 찾는 과정
    1. 평문 P로부터 대입 가능한 모든 키를 적용해보기: E(P, K1)
      • K1는 56bit이므로 $2^{56}$개의 암호문이 나옴
    2. 암호문 C로부터 대입 가능한 모든 키를 적용해보기: D(C, K2)
      • K2는 56bit이므로 $2^{56}$개의 암호문이 나옴
    3. 1번 과정과 2번 과정에서 생성된 암호문을 서로 비교
      • 같은 암호문을 찾으면 K1, K2를 찾은셈
  • 결론적으로 $2^{56}+2^{56}$번 암호문을 생성하면 key를 찾을 수 있음
  • 56bit key를 2개 사용했음에도 $2^{57}$ key를 사용한것과 같은 효과


AES(Advanced Encryption Standard)

  • 1997년 NIST가 암호화 알고리즘을 공모
    • 리즈멘(Rijmen)과 대먼(Daemen)의 Rijndael 알고리즘 중 일부분이 AES로 선정
  • 128비트 암호화 블록
  • key 길이는 128, 192, 256 비트를 사용할 수 있음
  • 현재 가장 많이 사용되는 암호 알고리즘


기타 대칭키 암호 알고리즘

  • SEED : 국내에서 개발, ISO/IEC와 IETF로부터 암호화 표준 알고리즘으로 인정, 국내에서 많이 사용됨
  • ARIA : 국내에서 개발, 국가표준으로 지정
  • 양자 암호 : 복제 불가능성 원리, 측정 후 붕괴라는 특성을 사용, 양자 암호 채널을 통해 전달되는 정보가 도청되면 양자 상태가 변경되고 이러한 임의 변경이 데이터 전달에 오류를 일으켜 곧바로 도청을 알아차림
  • IDEA : 모든 연산이 16비트 단위로 이루어지도록 하여 16비트 프로세서에서 구현이 용이, 주로 키 교환에 사용
  • RC5 : 비교적 간단한 연산으로 빠른 암복호화 가능
  • Skipjack
  • LEA : 경량 환경에서 기밀성을 제공하기 위해 국내에서 개발, AES 대비 1.5 ~ 2배 성능


대칭키 암호 알고리즘의 장단점

  • 장점: 연산이 매우 빠름
    • 56bit DES를 1초에 깰 수 있는 기계로 128bit AES를 깨려면 149조년이 걸림 [NIST]
    • DES는 RSA보다 소프트웨어로 구현하면 100배, 하드웨어로 구현하면 10,000배 빠름 [RSA Fast 2012]
  • 단점
    • 키 교환(또는 분배)가 어려움
    • 사용자가 늘어날수록, 비밀키의 개수도 증가
      • N명이 서로 비밀 통신을 하기 위해서는, (n)(n-1)/2개의 비밀키 필요
암호학
Symmetric-key DES 3DES AES
This post is licensed under CC BY 4.0 by the author.