Elliptic Curve Cryptography(ECC)

사전 지식(not required)

Finite Field (유한체)

• 2개의 연산(여기서는 +, *로 가정)에 대해 다음 성질을 만족하는 요소의 집합
  1. 유한성(finiteness): 원소의 개수가 유한
  2. 폐쇄성(closure): 연산의 결과도 동일 집합의 원소
  3. 결합성(associativity): a+(b+c)=(a+b)+c, a*(b*c)=(a*b)*c
  4. 교환성(community): a+b=b+a, a*b=b*a
  5. 분산성(distribution): a*(b+c)=a*b+a*c
  6. 항등원(identify) 존재: 각 요소 a에 대해 덧셈 항등원과 곱셈 항등원 존재
  7. 역원(inverse) 존재: 각 요소 a에 대해 덧셈과 곱셈 역원이 존재. 단, 덧셈 항등원에 대한 곱셈 역원은 존재하지 않음
• 대표적인 Finite Field: $Z_p$($p$는 소수)

Galois Field

• Finite Field의 원소 개수는 항상 $p^n$개이다. ($p$는 소수)
• Finite Field를 GF($p^n$)으로 표시. $p^n$은 요소의 개수

Modern cryptography

• $n$ 비트 블록 단위로 암호화 수행 (블록 암호화)
  • 암호문도 같은 크기의 블록으로 나온다.
• $n$ 비트를 암호화하면 나올 수 있는 경우의 수는 $2^n$ 이다.
  • GF($2^n$)에서 암호 및 복호 연산
• 주로 모듈러 덧셈/뺄셈, 곱셈/나눗셈 연산을 수행한다.

Elliptic Curve

타원 곡선(Elliptic Curve)

• 기본 방정식
  • $y^2=x^3+ax+b$
  • $y$축에 2차, $x$축에 3차인 특수 방정식
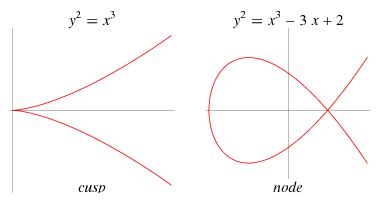
• 비특이 타원 곡선(non-signular elliptic curve)을 사용
  • $4a^3+27b^2 \ne 0$ 을 만족하는 타원 곡선
  • 첨점(sharp point), 교차점(intersection point)가 존재하지 않는 타원 곡선
• 우리가 보통 알고있는 타원 모양이 아님
  • 초기에는 타원 둘레 길이를 구하기 위해 만들었었음

(왼) 첨점이 존재 (오) 교차점이 존재

• 비특이 타원 곡선의 특징
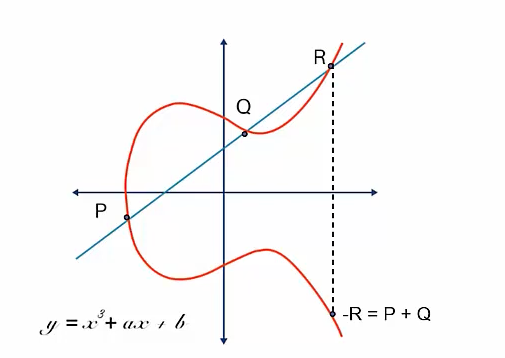
  • $x$축 상에서 $y$의 값이 정확하게 대칭
  • 두 점 P와 Q를 연결하는 직선은 반드시 다른 한 점(R)을 연결
  • P와 Q가 동일할 때도 성립: 접선

타원 곡선 점(Point)

• 점 $P=(x, y)$ : $x$는 $x$축의 값, $y$는 $y$축의 값
• 점 $0 = (x, 0)$ : $y$축의 값이 $0$인 점(영점)
• 점 $-P = (x, -y)$ : $P$의 $x$축 상의 대칭점
  • 비특이 타원 곡선에서 반드시 존재

타원 곡선 점 덧셈

• 정의
  • 직선으로 연결되는 점 $P, Q, R$에 대해, $P+Q+R=0$
• $P+Q = -R$
• $R+(-R) = 0$
  • $y$축에 대칭인 직선은 타원 곡선과 만나지 않음 = ‘무한점’
  • ‘무한점’의 대칭점을 ‘영점’으로 정의

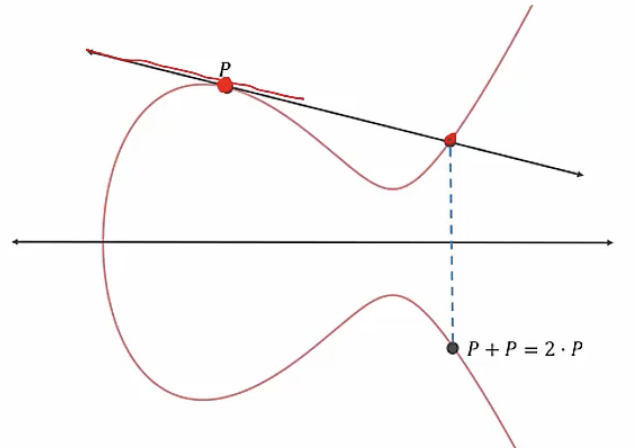
• $P+P=2P$
  • $P$의 접선과 만나는 점의 대칭점

타원 곡선 점 곱셈

• 동일점 덧셈과 스칼라 곱셈 연산
  • $P+P+\dots+P=kP$
  • 점 $P$의 $k$ 스칼라 곱
• 타원 곡선에서는 점과 점의 곱이 아니라, 점과 스칼라의 곱을 의미한다.

타원 곡선 점 연산 성질

• 덧셈과 스칼라 곱셈: 결합법칙, 교환법칙, 분배법칙이 만족함
• 항등원, 역원
  • 덧셈 항등원 : $0$
  • P의 덧셈 역원 : $-P$
  • 곱셈 항등원 : $1$
  • 곱셈 역원 : $P^{-1}$

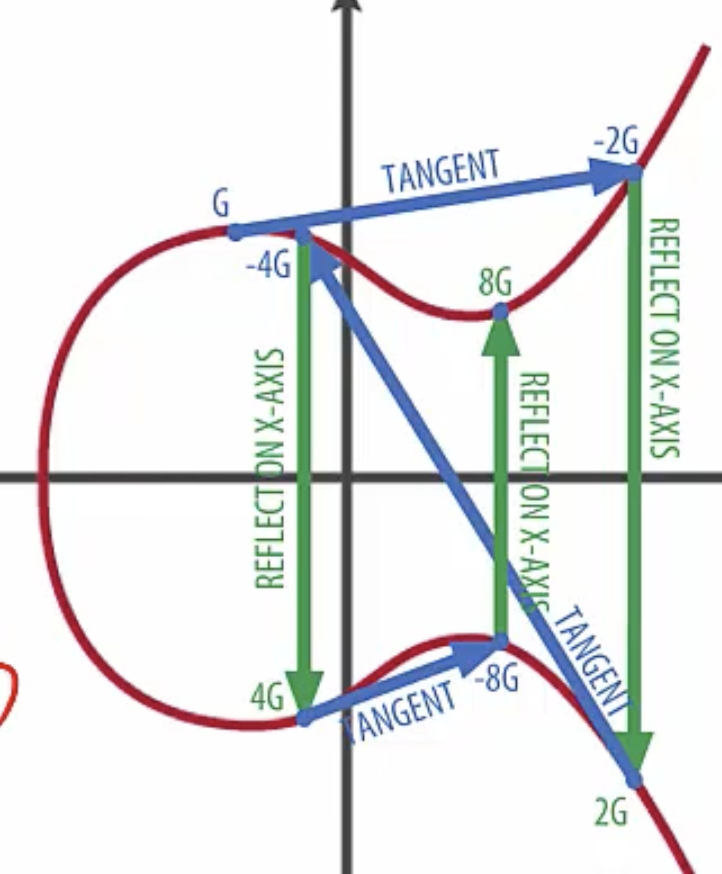
배가 연산(Doubling operation)

• 스칼라 곱을 빠르게 계산할 수 있음
• 2G = G + G
• 4G = 2G + 2G
• 8G = 4G + 4G
• $2^n$G 덧셈 횟수 = $n$

Double-add 알고리즘

• 빠르게 덧셈 연산하기
  • $k_{\max}$ = $n$ 비트 이진수의 최댓값 = $2^{n-1}+2^{n-2}+\dots+2^{0}$
  • $k_{\max}$G = $2^{n-1}$G + $2^{n-2}$G + $\dots$ + G
  • $k_{\max}$G 연산 횟수 = 배가 연산 (n-1)회 + 덧셈 연산 (n-1)회 = 2(n-1)회
• $k$가 256비트 값인 경우
  • $k$G의 최대 연산 횟수 = 255+255=510회
• 결론
  • 비특이 타원 곡선에서 알려진 점 G에 대해 $k$G는 쉽게 계산이 가능하다.
• 브루트포스로 계산하려면?
  • 최대 $2^n-1$번 연산을 수행해야 한다.

타원 곡선 이산 대수 연산

• 타원 곡선 이산 대수 문제
  • $K=x$G에서 $K$와 G가 주어질 때 $x$를 구하는 문제
• 타원 곡선 이산 대수 문제의 해법
  • 점 $K$로부터 점 G를 빼는 연산을 반복 수행
  • 알려진 빠른 계산 방법이 없음
  • 전통적인 지수 연산의 이산 대수 문제에 비해 훨씬 어려움
• $x$가 $n$비트 값인 경우
  • 최대 $2^n$회의 뺄셈 연산 수행
  • $x$의 값이 커지면 매우 어려운 문제

모듈러 연산

• (다른 암호 알고리즘과 비슷하게) Finite field 상의 타원곡선을 사용한다.
  • 컴퓨터에서는 실수(real number)와 음수, 무한값 등을 다루기 힘들다. 때문에 모듈러 연산이 팔방미인
• Elliptic Curves in Real domain
  • $\lbrace (x, y) \in \mathbb{R}^2 \vert y^2 = x^3+ax+b, 4a^3+27b^2 \ne 0 \rbrace \cup \lbrace 0 \rbrace$
• Elliptic Curves in Finite domain
  • $\lbrace (x, y) \in (\mathbb{F}_p)^2 \vert y^2 = x^3+ax+b \mod p, 4a^3+27b^2 \ne 0 \mod p \rbrace \cup \lbrace 0 \rbrace$, $p$는 소수
• 모듈로 $p$ 타원 곡선
  • 동일점 덧셈과 스칼라 곱셈 연산에 대해 GF($2^n$) [갈로아 필드]
  • 유한성, 폐쇄성, 결합성, 교환성, 분산성, 항등원, 역원이 모두 만족한다.

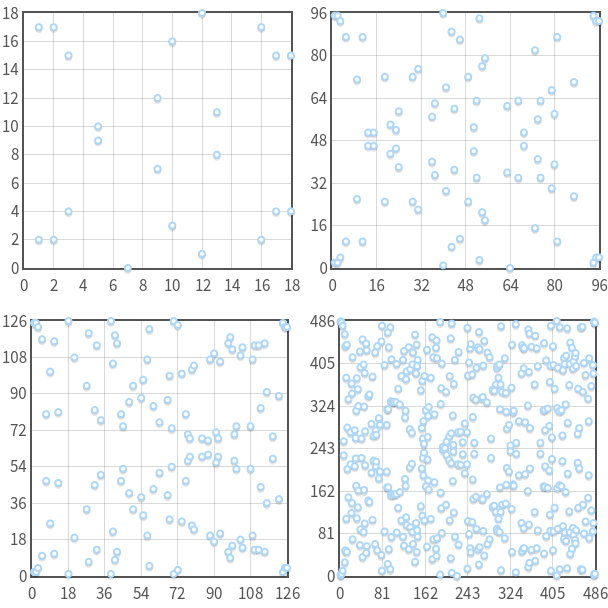Finite domain에서 Elliptic Curves가 표현하는 Rational points(왼쪽 위부터 시계방향으로 p=19, 97, 127, 487)

• 이때 mod $p$를 적용하여 얻어진 rational points의 개수와 $p$는 같지않다.
  • 이 개수를 구하는 방법은 Schoof’s algorithm을 이용하면 된다.
  • 이와 같은 가능한 점의 개수를 Order of the group($N$)이라고 한다.
• 임의의 한점을 골라서 같은 좌표를 더하는 연산(doubling)을 수행하면 $N$개의 점을 모두 순환하지는 않는다.
  • 예를 들어, $y^2=x^3+2x+3 \mod 97$의 $N$은 100이다.
  • 하지만 $P=(3, 6)$을 연속해서 배가연산을 수행하면 (80, 10), (80, 87), (3, 91), (Inf, Inf), (3, 6)와 같이 순환하게 된다.
  • 이와 같은 좌표 $P$를 Generator 또는 Base pointer 라고 하고, 순환 그룹을 Cyclic subgroup($n$)라고 한다.
• 타원 곡선을 암호에 이용하기 위해서는 큰 소수인 Cyclic subgroup $n$을 가지는 적절한 Generator $P$를 찾아야 한다.
  • 실제로는 적절한 $n$을 찾은 후 이를 만족하는 $P$를 선정하는 방식을 사용

ECC

Elliptic curve domain parameter (public information)

• p: 모듈러 값. Prime number
• G: Generator point. $(X_G, Y_G)$
• a, b: 타원 곡선 $y^2=x^3+ax+b$ 의 $a, b$ 값
• n: Order of subgroup. G를 계속 더했을때 순환하는 그룹의 개수
• N: Elements number in Finite field
• h: Cofactor of subgroup (N/n)

타원 곡선 이산 대수 문제(ECDLP)

• Elliptic Curve Discrete Logarithm Problem
• 타원 곡선 상의 알려진 점(P)을 더하여 새로운 점을 계산하는 횟수를 나타내는 값($k$)을 개인키로 하고,
• P를 $k$번 더해 생성되는 새로운 점에 해당하는 값($k$P)을 공개키로 정의할 때, 공개키($k$P)로부터 개인키($k$)를 계산하는 문제

• 사실 DL과 별로 상관없지만, 기존 암호시스템 관습에 따라 ‘ECDLP’라고 부른다.

• 현재까지 빠른 계산 방법이 거의 알려지지 않음
  • 브루트포스에 의존
• [소인수 분해]나 [지수 함수 이산 대수 연산]에 비해 같은 크기의 키를 사용할 때 훨씬 많은 수의 연산이 필요함

보안 강도: key size

• 같은 보안 강도를 가질 때 대칭키, RSA, ECC의 key size 비교
• NIST Recommendations

Symmetric	RSA	ECC
80	1024	160
112	2048	224
128	3072	256
192	7680	384
256	15368	512

응용

• 디지털 서명
  • Elliptic Curve Digital Signature Algorithm (ECDSA)
  • Edwards-curve Digital Signature Algorithm (EdDSA)
• 1회용 대칭키(새션키) 생성을 위한 Diffie-Hellman 알고리즘
  • Elliptic Curve Diffie–Hellman (ECDH)
  • 전통적인 Diffie-Hellman: 모듈러 지수 연산
  • 성능 향상을 위해 타원 곡선을 함께 사용
• 암호화
  • Elliptic Curve Integrated Encryption Scheme (ECIES)
• 최근 TLS, 비트코인 등에서 자주 사용된다.

타원 곡선 암호

• ECC를 사용하기 위해서는 사전에 결정이 필요한 파라미터들이 있다.
  • 어떤 타원곡선을 사용? p는 어떤값? G는?
  • 일반적으로 직접 생성해서 사용하지 않고 NIST, SECG 등에서 발표한 표준 곡선을 사용한다.
  • 직접 정의하는 것이 오래걸릴 수 있고, 잘못 선택하면 보안상 문제가 있을 수 있기 때문이다.
  • NIST P-256, NIST P-384, secp256k1, secp384r1, sect283k1 등
• Standard curve database
• secp256k1 표준
  • $a=0, b=7, p=2^{256}-2^{32}-2^9-2^7-2^6-2^4-1$
  • ‘256’의 의미 : 256bit 크기의 소수 p를 사용한다.
  • ‘k’의 의미 : Koblitz 타원곡선
  • 비트코인을 비롯한 많은 암호화폐가 secp256k1을 사용
• 개인키
  • 정수 $k$ (스칼라)
• 공개키
  • $k$G ( = 점 $K$)
  • 어떤 타원곡선인지, p, G 등 다른 파라미터도 사실상 모두 공개된 정보

Elliptical Curve Digital Signature Algorithm(ECDSA)

• Senario
  • Alice가 Bob에게 메시지를 보낼 때 sign 수행 (using private key $d_A$)
  • 이때 hash 함수를 메시지 m에 적용시켜 digest message를 만듦 (hash(m)=$z$)
  • Bob은 메시지 검증 수행 (using public key $H_A$)
  • $H_A=d_AG$
  • 타원곡선 파라미터, $G, n, H_A$는 모두 public information. $d_A$만 private.
• Signing process (Alice)
  1. random interger k in $\lbrace 1, \dots, n-1\rbrace$ ($n$ is the subgroup order)
  2. Calculate the point $P=kG$ ($G$ is base point of the subgroup)
  3. Calculate the number $r=x_p \mod n$ ($x_p$ is the $x$ coordinate of $P$)
  4. If $r=0$, then choose another $k$ and try again
  5. Calculate $s=k^{-1}(z+rd_A) \mod n$
  6. If $s=0$, then choose another $k$ and try again
     • The pair (r, s) is the signature
• Verifying signature(Bob) : 현재 Bob은 $r, s, z, H_A$를 알고있는 상황
  1. Calculate the interger $u_1=s^{-1}z \mod n$
  2. Calculate the interger $u_2=s^{-1}r \mod n$
  3. Calculate the point $P=u_1G+u_2H_A$
  4. The signature is valid only if $r=x_p \mod n$

Correctness

\[P=u_1G+u_2H_A=u_1G+u_2d_AG=(u_1+u_2d_A)G\] \[P=(u_1+u_2d_A)G=(s^{-1}z+s^{-1}rd_a)G=s^{-1}(z+rd_A)G\]

$s=k^{-1}(z+rd_A) \mod n$이므로 $k=s^{-1}(z+rd_A) \mod n$이다.
따라서 $P=s^{-1}(z+rd_A)G=kG$

Elliptical Curve Diffie-Hellman(ECDH)

• 전통적인 Diffie-Hellman의 문제점
  • 모듈러 지수 연산을 통해 공개키를 만들기 때문에 그 과정에서 시간이 오래 걸린다.
  • 키의 크기가 크다.
• 사용자 A
  • 개인키: $k_A$
  • 공개키: $K^+_A=k_AG$ → B에게 전송
• 사용자 B
  • 개인키: $k_B$
  • 공개키: $K^+_B=k_BG$ → A에게 전송
• 사용자 A의 대칭키
  • $k_AK_B^+=K_{AB}\mod p$
• 사용자 B의 대칭키
  • $k_BK_A^+=K_{AB}\mod p$
• 증명
  • $k_AK_B^+=k_A(k_BG)=k_B(k_AG)=k_BK_A^+ \mod p$

Reference

공개키암호2_타원곡선암호(ECC)(박승철 교수)
Application of Elliptical Curve Cryptography (ECC): ECDH & ECDSA(유호영 교수)