Cryptographic Protocols

Posted Dec 24, 2024 Updated Dec 27, 2024

By I Think So 20 min read

본 포스팅에서는 암호를 이용한 여러 프로토콜을 살펴보고자 한다. 사실 각 주제마다 방대한 양이지만 여기서는 가볍게 컨셉만 확인하자

Massey-Omura

공개 또는 서로 공유하는 정보가 아무것도 없는 암호
- 하지만 state를 유지해야하기 때문에 실용성이 낮다.
Suitcase Example
- Goal: A가 B에게 안전하게 가방을 보내고 싶다.
- A가 가방에 자신의 자물쇠로 잠금
- B는 가방에 자신의 자물쇠로 다시 잠가서 A에게 보냄
- A는 자신의 자물쇠를 열고 B에게 다시 보냄
- B는 자신의 자물쇠로 가방을 연다.
Detail
- Setting
  - Shared $p$
  - A’s Secret: $e_a, d_a, e_a\times d_a=1 \mod {p-1}$
  - B’s Secret: $e_b, d_b, e_b\times d_b=1 \mod {p-1}$
- A → B : $m^{e_a} \mod p$
- B → A : $(m^{e_a})^{e_b} = m^{e_ae_b} \mod p$
- A → B : $(m^{e_ae_b})^{d_a} = m^{e_b} \mod p$
- B : $(m^{e_b})^{d_b}=m \mod p$

하나의 비밀정보를 다수의 비밀조각으로 분할하여 다수의 신뢰할 수 있는 사람들에게 공유
예시 알고리즘: $(k,n)$-threshold scheme (또는 Shamir’s Secret Sharing)
- $n$개의 비밀조각 중에서 $k$개 이상의 비밀조각만 있으면 원래의 비밀 정보를 복원할 수 있는 시스템
- $k-1$차 다항식 이용
How?
1. 식 생성 : $f(x)=a_{k-1}x^{k-1}+a_{k-2}x^{k-2}+\cdots+a_{1}x^{1}+S$
  - $a_i$ is random
2. 서로 다른 $(i, f(i))$을 $n$개 만들어 배분
3. 점 $k$개가 있으면 $f(x)$를 구할 수 있다. → $S$를 구할 수 있음
  - 연립방정식 또는 Lagrange 보간법 이용
  - 하지만 $k-1$개의 점이 있으면 $S$를 전혀 알 수 없다.

예시: (3, 6) threshold scheme

정보를 6개의 비밀 조각으로 나눔, 3개 이상의 비밀 조각이 모이면 정보 획득 가능
비밀 조각 만들기
- $S = 1234, a_1 = 166, a_2 = 94$
- $f(x) = 94x^2+166x+1234$
- $s_0 = (1, 1494), s_1= (2, 1942), s_2 = (3, 2578), s_3= (4,3402), s_4 = (5,4414), s_5 = (6,5614)$
비밀복원(Reconstruction)
- 3개 이상의 조각이 있으면 $f(x)$을 만들 수 있다.

Bit Commitment

Fair Coin Flip

온라인 상에서 동전 던진기

문제
- Alice와 Bob이 전화상으로 통화를 하고 있다
- Alice가 동전을 던진다. 결과는 앞면(head) 또는 뒷면(tail)
- Bob이 앞면인지 뒷면인지 추측한다 (guessing)
- Alice가 정답을 알려준다
- Bob이 Alice가 정답을 얘기했음을 확인한다.
Bob은 Alice가 동전을 던지는 것을 눈으로 직접 확인하지 않고, Alice가 동전을 던져 나온 결과를 어떻게 믿을 수 있을까?
- Bit Commitment 필요!

Coin Flipping using One-Way Functions

Alice chooses a random number $x$
Alice computes $y = f(x)$
- 예를 들어 $f(x)$는 Hash(x)
- 사실 종류도 많고 방법도 다양하다.
Alice sends $y$ to Bob
Bob guesses whether $x$ is even or odd, and sends his guess to Alice
Alice announces the result of the coin flip, and sends $x$ to Bob
Bob confirms that $y = f(x)$
Bit Commitment는 온라인 상에서 안전한 데이터 송수신을 위해 기본이 되는 프로토콜 중 하나이다. 근데 목적이 암호화와는 조금 다르다. 두 사용자가 대화형으로 메시지를 주고받는 과정에서 서로 속이지 않는지 진위여부를 판단하기 위해 사용된다.

Bitcoin

여기서는 비트코인의 기술인 블록체인에 중점을 두어 살펴봅니다.
- 세부적인 디테일은 현재 거래되는 비트코인과 다를 수 있습니다.
Java를 이용하여 Blockchain 기술을 이해하시고자 하는 분은 아래 사이트를 참고해주세요.

거래 (transaction)

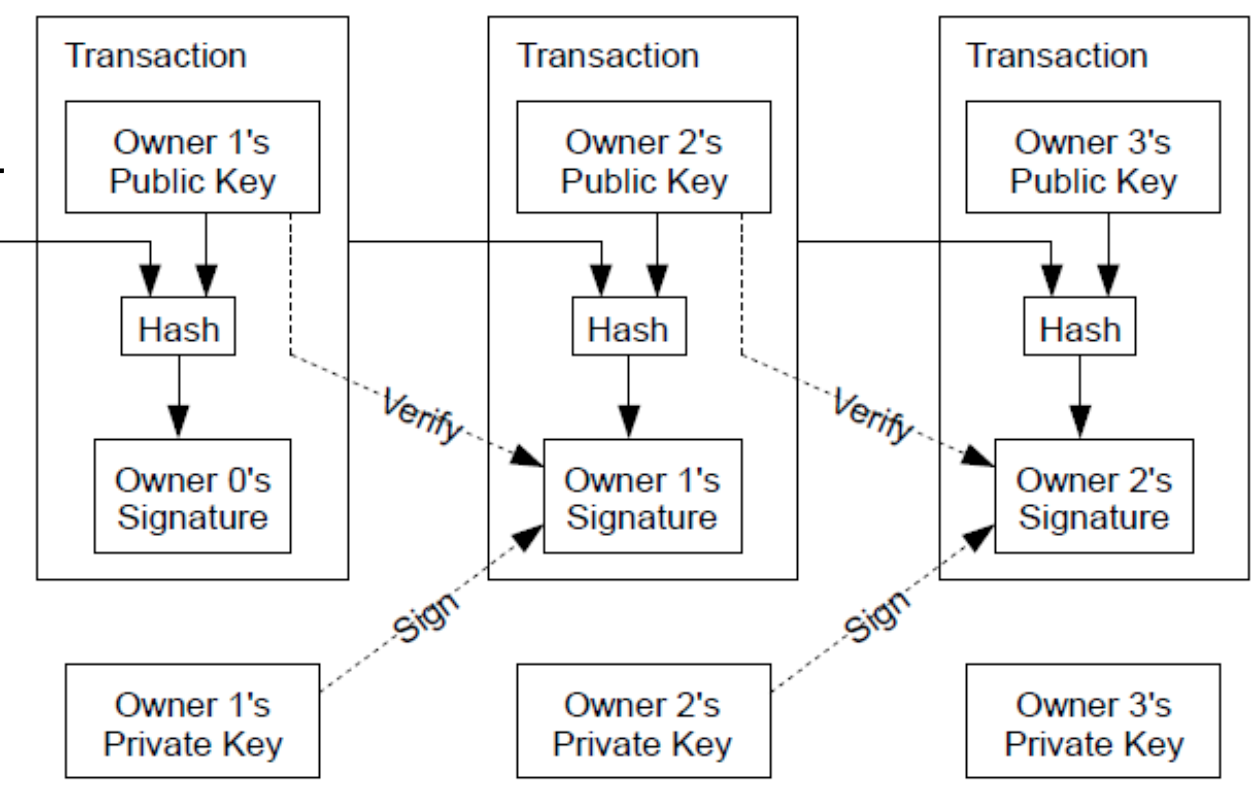
A가 B에게 비트코인을 이체
- 코인은 ‘실제 돈’이 아니라, ‘A가 B에게 이체를 했다라는 사실 증명들의 체인’이다.
A는 “Hash(이전 거래내역들의 체인 + 현재 거래내역 + B의 공개키)”을 A의 개인키로 전자서명 생성
- 사용자 인증
- 거래 내역의 위조 불가능성
P2P 서버에 broadcast

  
public class Wallet {

    public PrivateKey privateKey;
    public PublicKey publicKey;

    public Map<String, TransactionOutput> UTXOs; // 지갑에 담긴 미사용 transaction
    ...
}

Transaction chain
- 예를 들어, 100 비트를 전송하고자 한다면
- 50btc가 담겨있는 있는 transaction, 30btc가 담겨있는 있는 transaction, 30btc가 담겨있는 있는 transaction
- 위 3개의 transaction이 모여서 1개의 transaction과 남은 차액(10btc)이 담긴 transaction이 생성된다.

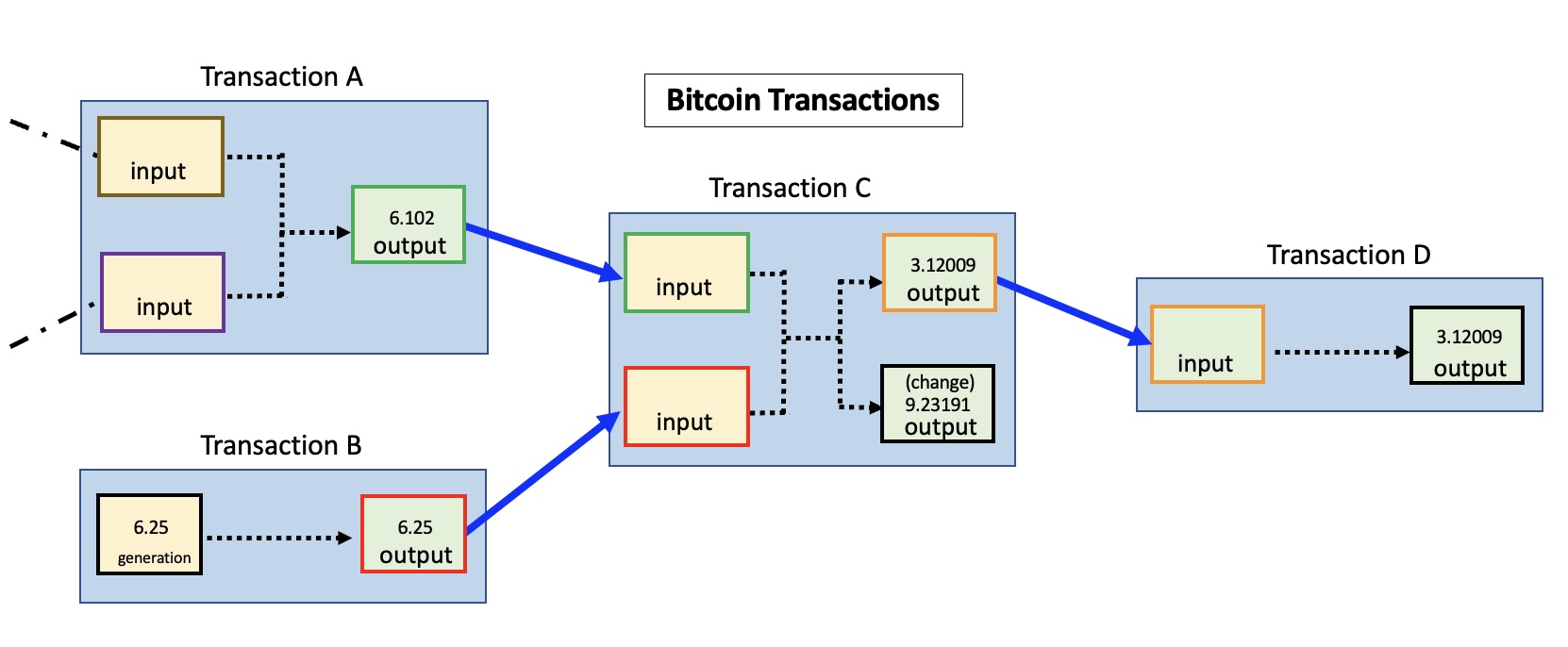https://en.bitcoin.it/wiki/File:Bitcointransactions.JPG

  
public class Transaction {

    public String transactionId; // Contains a hash of transaction
    public PublicKey sender;     // Senders address/public key.
    public PublicKey reciepient; // Recipients address/public key.
    public float value;          // Contains the amount we wish to send to the recipient.
    public byte[] signature;     // This is to prevent anybody else from spending funds in our wallet.

    public List<String> inputs;  // 이 거래를 만들기 위한 트랜잭션들
    public List<String> outputs; // 이 거래 이후에 만들어진 트랜잭션들
    ...
}

Proof of Work (작업 증명)

특정 단위로, P2P에 broadcasting된 모든 거래내역들을 모아서 하나의 block을 생성
현재까지 생성된 모든 Block들에 대한 chained-timestamp 생성
- Block : 일정 시간 동안 발생한 모든 transaction
- Blockchain
작업 증명(Proof of Work): 새로운 block에 대한 해시 값을 찾아내는 작업
- hash(데이터 + 랜덤값) = 특정 조건을 가진 값
- 채굴(mining): 작업 증명을 수행 하는 과정
  - ‘랜덤값’은 무작위 대입하면서 찾자 → 땅을 파자 → 채굴
작업 증명이 끝나야 트랜잭션들을 묶어 새로운 block을 만들고 채이닝 할 수 있다. → 누가 작업 증명을 할건데? → incentive를 지급하자 = 비트코인
- 한 블록에 대한 작업 증명이 완료되어야, 실제 블록 내에 포함된 모든 거래에 대한 이체가 완료됨
- 그래서 비트코인 전송시간은 대략 10분 이상 걸린다.
새로운 block에 대한 해시 값을 찾아낸 사람만이 chained-timestamp 생성 가능
- 누구나 작업 증명에 참여할 수 있지만, 최초로 작업 증명을 끝낸 사람이 chained-timestamp 생성
- 작업 증명을 끝낸 최초의 사용자에게 incentive 지급
  - 새로운 비트 코인 발행: 중앙은행이 아닌 채굴자가 화폐 제조 및 발행 (화폐 제조 권한이 분산)
  - 사용자들로 하여금 작업 증명에 능동적 참여 유도
블록 해시의 조건: 앞자리 18자리가 모두 0이어야 함
- Hash(이전 블록의 해시 값 + 현재 블록의 거래 내역들 + Nonce)
- 채굴 = Nonce를 찾는 과정
- 수행한 결과 앞자리 18비트가 모두 0으로 채워져야 함
  - 난이도에 따라 다름
- Nonce를 먼저 찾는 사람이 성공!
  - hash 함수의 특성상 output을 보고 input을 추정하기 힘들다.
  - 따라서 일반적으로 브루트포스 방식으로 Nonce를 대입해본다.

  
public class Block {

    public String hash;         // 예를 들어, SAH(previousHash + timeStamp + nonce + merkleRoot)
    public String previousHash; // for Block chain!!
    public String merkleRoot;
    public List<Transaction> transactions;
    public long timeStamp;
    public int nonce;           // 이 값을 찾기 위해 채굴 과정이 필요함
    ...
}

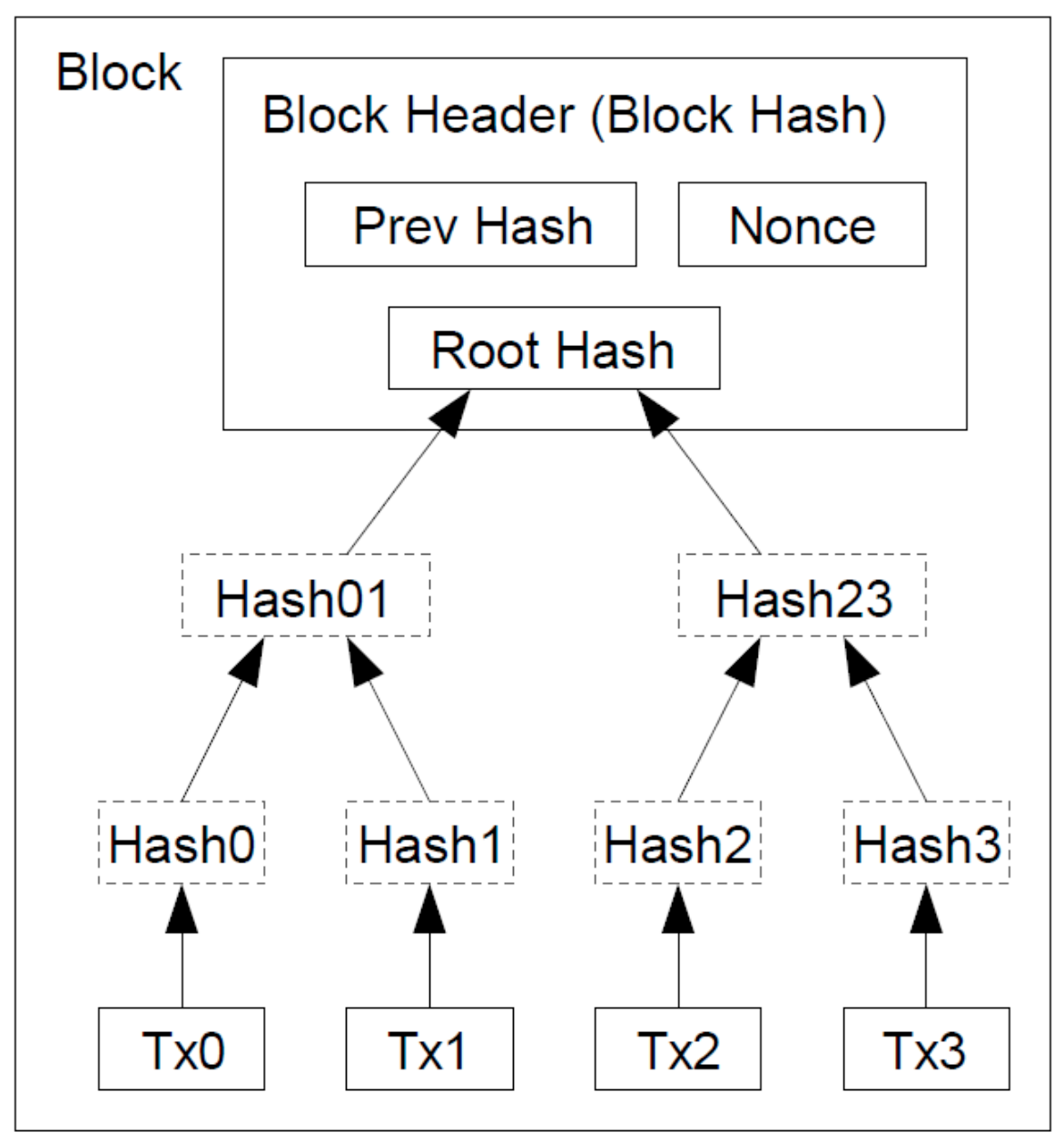
Merkel Tree

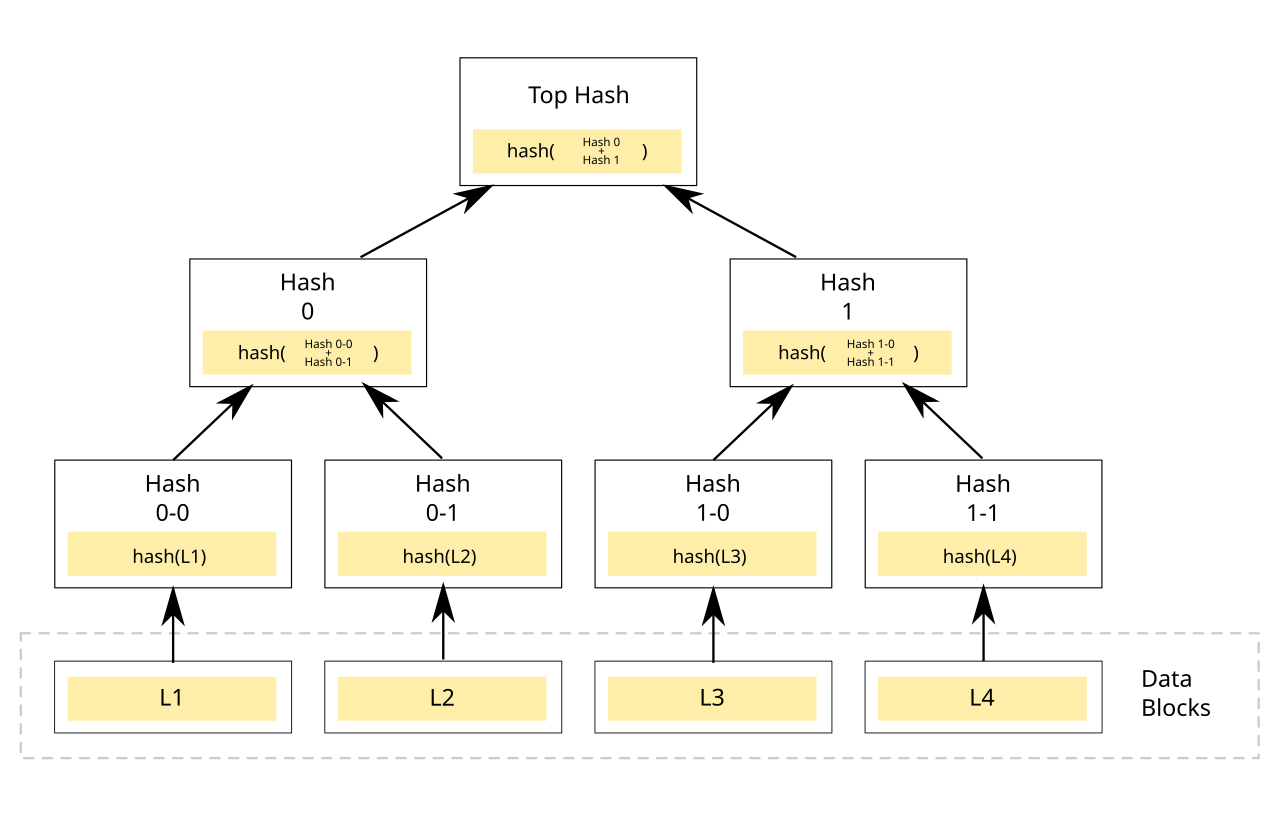https://en.wikipedia.org/wiki/Merkle_tree

2개씩 묶어 새로운 Hash 생성. 최종적으로 1개의 Root Hash(merkleRoot) 생성
- 이때 중간에 만들어졌던 중간 해쉬값들도 모두 Block에 저장한다.(option)
트랜잭션 검증하기
1. 트랜잭션의 전자서명을 통해 ‘어떤 사람’이 만들었다는 인증 수행
2. 해당 트랜잭션에서 만든 해쉬와, 나머지 중간 해쉬값들을 이용해 Root Hash를 계산한다.
3. Block Hash를 계산 후 비교
왜 트랜잭션 자체를 저장하지 않고, 중간의 Hash 값만 Block에 저장하나요?
- 트랜잭션은 사이즈가 너무 크다. (전자서명 등 여러가지가 들어있음)
- Hash 값은 고정된 크기이므로 효율적이다.
  - 예를 들어, 해쉬 값은 160bit, 10분간 1024개의 거래가 발생, 1개 블록은 10분간의 거래를 묶는다고 하면
  - 1개 블록 = (1024+512+64+32+16+8+4+2+1)*160bit = 약 41KB
  - 1시간 = 6 * 41KB
  - 1일 = 24 * 6 * 41KB
  - 1년 = 365 * 24 * 6 * 41KB
  - 10년 = 10 * 365 * 24 * 6 * 41KB = 21.5496GB

Bitcoin의 안전성

거래 내역에 대한 작업 증명(proof of work) 생성이 안전성 보장

가장 긴 blockchain이 가장 정확
- ‘길다’는 표현의 의미는 ‘몇 개의 블럭 해쉬를 포함하는 블럭이나?’ 이다.
- 실시간으로 모든 블락이 공유되는 상황
- 가장 긴 blockchain을 기준으로 새로운 blockchain 생성
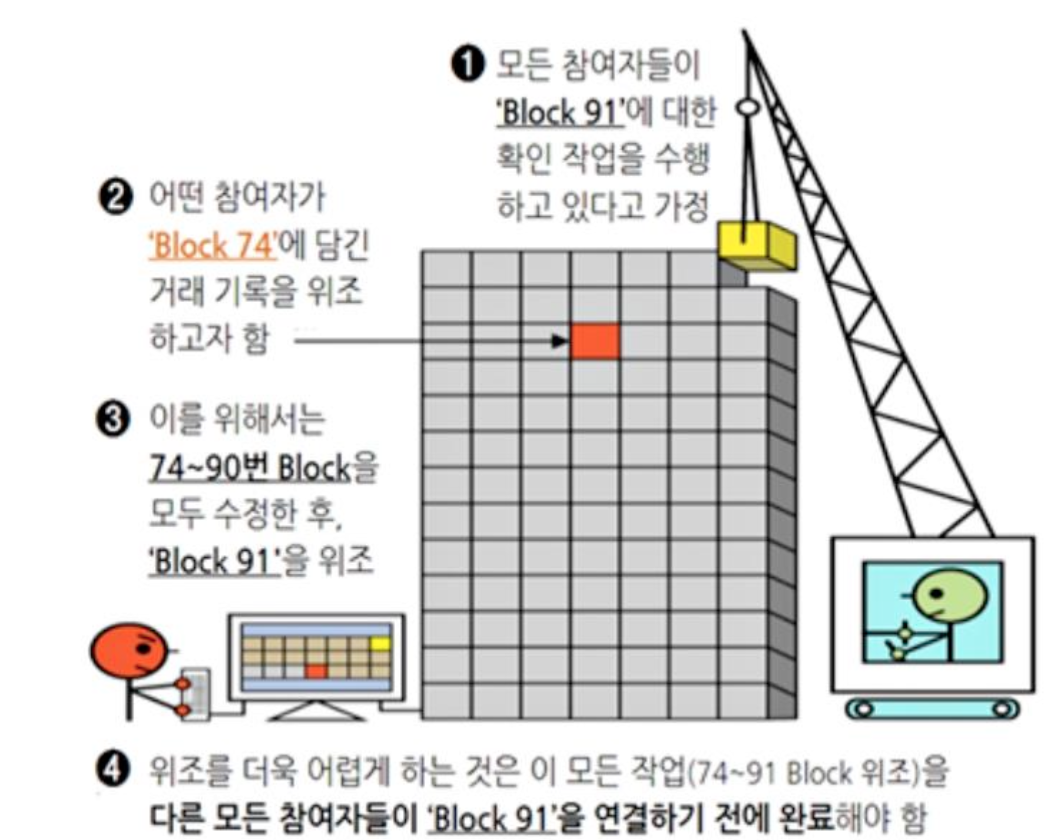
해커가 과거 거래 내역을 위조하는 것은 불가능
- 과거 거래내역을 포함하는 블록부터 이후에 모든 블록을 새로 위조해야 함
  - 정확한 Blockchain이 계속해서 갱신
- 공격 블록부터 이후 모든 블록 추가 후에 최신블록까지 따라잡을 수 없음
정확히 말하면 블럭을 만들려면 작업증명(채굴)을 해야하는데, 빠른속도로 현재 정상적으로 만들어지는 체인보다 빠르게 만드는게 불가능하다는 의미이다.

IEEE Spectrum(2015.7)

Zero Knowledge Proof

$P$(증명하고 싶어하는 사람) , $V$(확인하려는 사람)
$P$는 자신이 비밀정보 $X$를 안다는 것을 $V$에게 증명하려고 한다.
가장 쉬운 방법: $V$에게 $X$를 보여줘서 증명함
- 문제점 : $V$에게 비밀정보를 넘겨줘야 한다.
이 프로토콜의 최종 목적
- $V$에게 $X$의 일부 정보라도 주고 싶지 않다.(no transfer)
- ‘$P$가 $X$를 알고 있다’는 정보만 주고 싶지, $X$ 자체를 주고 싶지는 않다.
- 또한 $X$를 모르는 제3자는 매우 높은 확률로 증명에 실패해야 한다.
왜 이 프로토콜을 사용할까?
- 인증서로 로그인할 때 이미 어느정도 구현되어 있다.
- 비밀번호 로그인은 구현이 안되어 있음
  - 내가 비밀번호를 안다는 것만 알려주고 싶지 비밀번호는 알려주고 싶지 않음
  - 비밀번호를 안다는 것을 가장 쉽게 증명하는 방법은 비밀번호 자체를 넘겨주는 것
  - 하지만 가짜 사이트, 가짜 프롬프트, 카드 리더기 복사.. 등의 문제가 발생함
- 이론적으로 완벽을 만들기 위함
  - 실용적이진 않음(실제로 사용은 안함)
  - RSA의 경우 NP-Complete가 아니지만 실용적이기 때문에 사용

Zero Knowledge Proof of Graph Isomorphism

Graph Isomorphism Problem : 두 그래프는 동형인가?
- 노드 번호를 잘 rename하면 완전히 두 그래프를 같게 할 수 있냐?
- NP-Complete 문제이다.
  - node $n$개, edge $m$개
  - rename 방법: $n!$

Details of the Proof

공개된 정보 : $G_1, G_2$
- 두 그래프 $G_1, G_2$는 동형임
Secret Infomation$(X)$ : mapping between $G_1$ and $G_2$
- 두 그래프 자체는 공개되어도 괜찮지만, 매핑 정보는 비공개.
$G_1, G_2$를 만드는건 쉽다. (예를 들어 랜덤하게 $G_1$을 만들고 permutation시켜 $G_2$를 만든다.)
$P$가 $G_1, G_2$를 만들고, ‘그 매핑을 아는 사람은 나다’는 것을 증명
대략적인 알고리즘
1. $P$는 $G_1$을 rename해서 $G_{temp}$를 만들어 $V$에게 전달
  - $P$는 $G_1\leftrightarrow G_2 \leftrightarrow G_{temp}$ 매핑을 모두 안다.(자신이 $G_1, G_2, G_{temp}$를 만들었기 때문)
2. $V$는 $G_1\sim G_{temp}$ 또는 $G_2 \sim G_{temp}$ 의 매핑을 물어본다.
3. $P$는 mapping을 증명해준다.
  - 가짜 $P’$은 높은 확률로 여기서 실패
가짜 $P’$은 $G_1 \leftrightarrow G_2$ 매핑을 모르기 때문에 $G_1\sim G_{temp}$ 와 $G_2 \sim G_{temp}$ 중 최대 1개만 알 수 있다.
- 둘 다 안다는 건 사실상 $G_1 \leftrightarrow G_2$ 을 아는거나 마찬가지이기 때문
Round를 여러번 진행하면 $V$는 $P$가 $G_1$와 $G_2$ 사이의 매핑 정보를 정확히 알고있다고 인정

Why is it Zero Knowledge?

가장 중요한 핵심: no transfer
$V$가 그래프 매핑을 계산할 수 있는 경우도 있다.
- Round 1
  - $P \rightarrow V : G_{temp~1}$
  - $V \rightarrow P : G_1 \sim G_{temp~ 1}$ mapping 정보는?
  - $P \rightarrow V:G_1 \sim G_{temp~1}$ mapping을 알려줌
- Round 2
  - $P \rightarrow V : G_{temp~2}$
    - 이때 $G_{temp~1}=G_{temp~2}$ 이라면?
  - $V \rightarrow P : G_2 \sim G_{temp~ 2}$ mapping 정보는?
  - $P \rightarrow V:G_2 \sim G_{temp~2}$ mapping을 알려줌
  - $V$는 $G_1, G_2$의 mapping을 계산 할 수 있다.
Round 개수를 $n!$ 번 하면 분명 $G_{temp}$는 서로 겹치거나, $G_1$ 또는 $G_2$와 겹치는 경우가 발생한다.
- Round를 진행할 때마다 아주 조금씩 정보가 전달되는게 아닌가?
- 정보가 전달되는게 아니라, $V$가 계산하는거다.
$V$가 실제 $P$와 통신하는게 아니라, 자기 스스로 fake $P$를 만들어서 대화한것(Transcript)을 구별할 수 없다.
- 실제 $P$와 통신해서 만들어진 Transcript와 $V$ 혼자 만든 Transcript가 등장할 확률이 동일하다.
Why not used?
- 실용적이지 않음

실제 사용하는 알고리즘 (using RSA)

Zero Knowledge라는 증명은 없음
상황: 나(A)와 은행(Bank)와 거래
- 나 : $n, e$는 공개 정보, $p, q, d$는 비밀정보
- 은행 : 너가 $d$를 알고있다는 것을 증명하라
$d$를 은행한테 직접 전송하지 않고, 자신이 $d$를 알고있다는 사실을 어떻게 증명할 것인가
방법
1. 은행이 Random message $m$을 만들어서 나에게 전송
2. 나는 사인을 해서 $m^d$를 다시 은행한테 전송
3. 은행은 공개키 $e$를 이용해 signature verification
  - $m^{ed}==m$이라면 내가 $d$를 알고있다는 사실을 증명한 셈이다.

Massey-Omura와 유사
B가 A에게 메시지 $m$에 사인 요청. 단, $m$의 내용은 숨기고싶다.
구현 방법은 여러가지가 있음. 여기선 RSA를 응용한 버전 중 하나

B가 A한테 메시지 $m$에 대해 사인 요청
- 이때 B가 $m$을 자기 공개키로 암호를 걸어 보냄 ($m^{e_b}$ 전송)
A가 사인을 해서 다시 B에게 보냄 : $(m^{e_b})^{d_a}$
- A는 메시지 $m$을 모른 상태로 사인
B는 받아서 자기 비밀키로 복구 : $((m^{e_b})^{d_a})^{d_b}=m^{d_a}$

암호학

암호학 cryptography

This post is licensed under CC BY 4.0 by the author.

Cryptographic Protocols

Massey-Omura

예시: (3, 6) threshold scheme

Bit Commitment

Fair Coin Flip

Coin Flipping using One-Way Functions

Bitcoin

거래 (transaction)

Proof of Work (작업 증명)

Merkel Tree

Bitcoin의 안전성

Zero Knowledge Proof

Zero Knowledge Proof of Graph Isomorphism

Details of the Proof

Why is it Zero Knowledge?

실제 사용하는 알고리즘 (using RSA)

Blind Signature

Trending Tags

Massey-Omura

Secret Sharing

예시: (3, 6) threshold scheme

Bit Commitment

Fair Coin Flip

Coin Flipping using One-Way Functions

Bitcoin

거래 (transaction)

Proof of Work (작업 증명)

Merkel Tree

Bitcoin의 안전성

Zero Knowledge Proof

Zero Knowledge Proof of Graph Isomorphism

Details of the Proof

Why is it Zero Knowledge?

실제 사용하는 알고리즘 (using RSA)

Blind Signature

Trending Tags