BOJ-28276(Yawned-Zoned)
원래 특정 문제에 대한 포스팅은 지양하는 편이지만, 이 문제는 나를 너무 고생시킨 기념으로 포스팅한다.
주아이디어
기본적인 아이디어는 “매개 변수 탐색”이다. 주어진 C번 만큼만 끊어서, 특정 숫자((min+max)/2)만 하품하는 경우를 만들 수 있는지 확인하면 된다.
아마 대부분 이 아이디어까지는 금방 도달했으리라 생각한다. 사실 주아이디어를 떠올리는 건 가장 약한 놈이었다.
1
2
3
4
5
6
7
8
9
10
11
12
13
// 구현 편의상 board[0]은 모두 '0'으로 채웠다.
cin >> h >> w >> c;
board[0] = "";
for (int i = 0; i < w; ++i) board[0].push_back('0');
for (int i = 1; i <= h; ++i) cin >> board[i];
ll mn = 0, mxx = 1e12;
while (mn < mxx) {
ll mid = (mn + mxx) / 2;
if (ispossible(mid)) mxx = mid;
else mn = mid + 1;
}
cout << mxx;
구현
문제는 ispossible(mid)를 구현하는 일이었다.
가장 왼쪽 열부터 탐색을 시작하여, mid개가 넘는 집합이 생기면, (직전 열)~(현재 열) 사이에 칸막이를 두면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool ispossible(ll mid) {
int 사용한칸막이개수=0;
for(int x = 0; x < w; x++) {
for(int y = 1; y <= h; y++) { // 구현 편의상 board[1]부터 시작
// 집합 구현(merge, alloc 등)
if(집합크기의최대값 > mid){
// 칸막이 설치
사용한칸막이개수+=1;
if(사용한칸막이개수 > c) return false;
}
}
}
return true;
}
문제는 집합을 구현하는 것이다. 칸 개수의 최댓값은 10^12이다. 각 칸을 하나의 집합으로 두고, union-find 하면 메모리가 터진다. (또한 각 집합마다 집합 크기를 기록해야한다.)
하지만 조금만 생각해보면, 한 번에 다루는 집합의 최대 개수는 h개라는 것을 알 수 있다.
우리는 현재 열과 직전 열만 고려하면 되기 때문이다.
예시
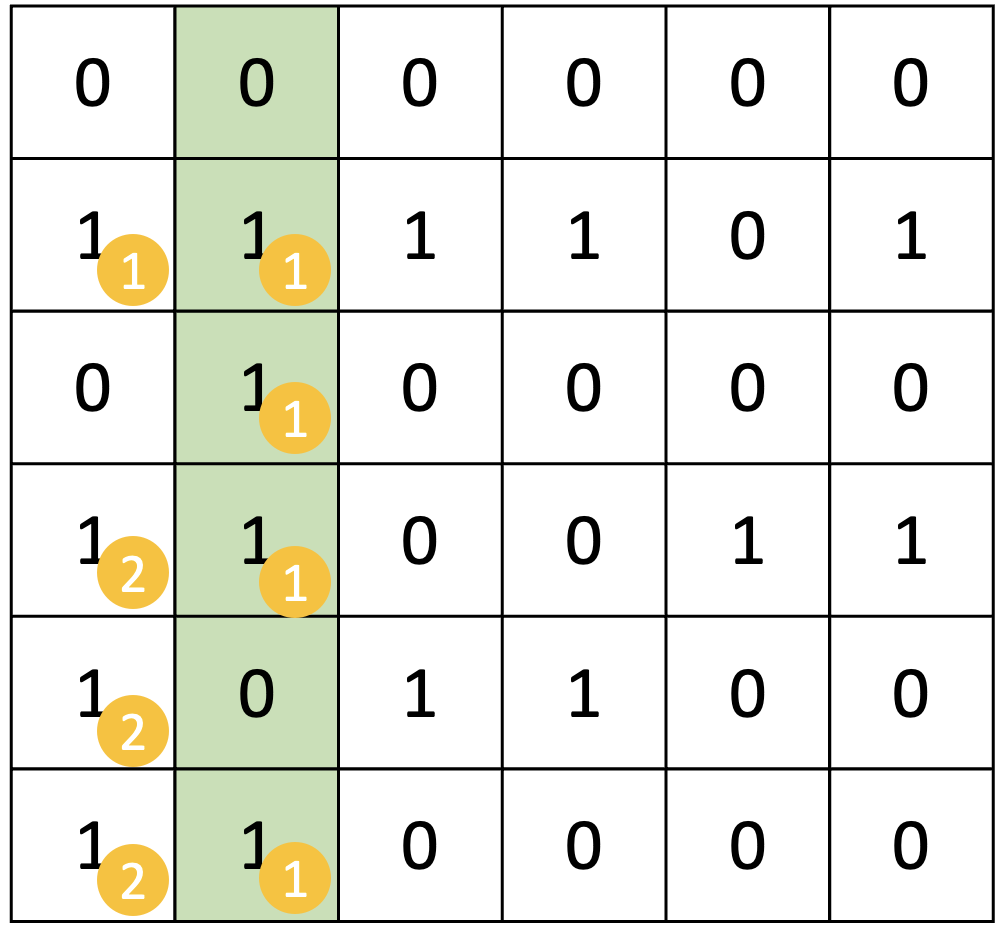
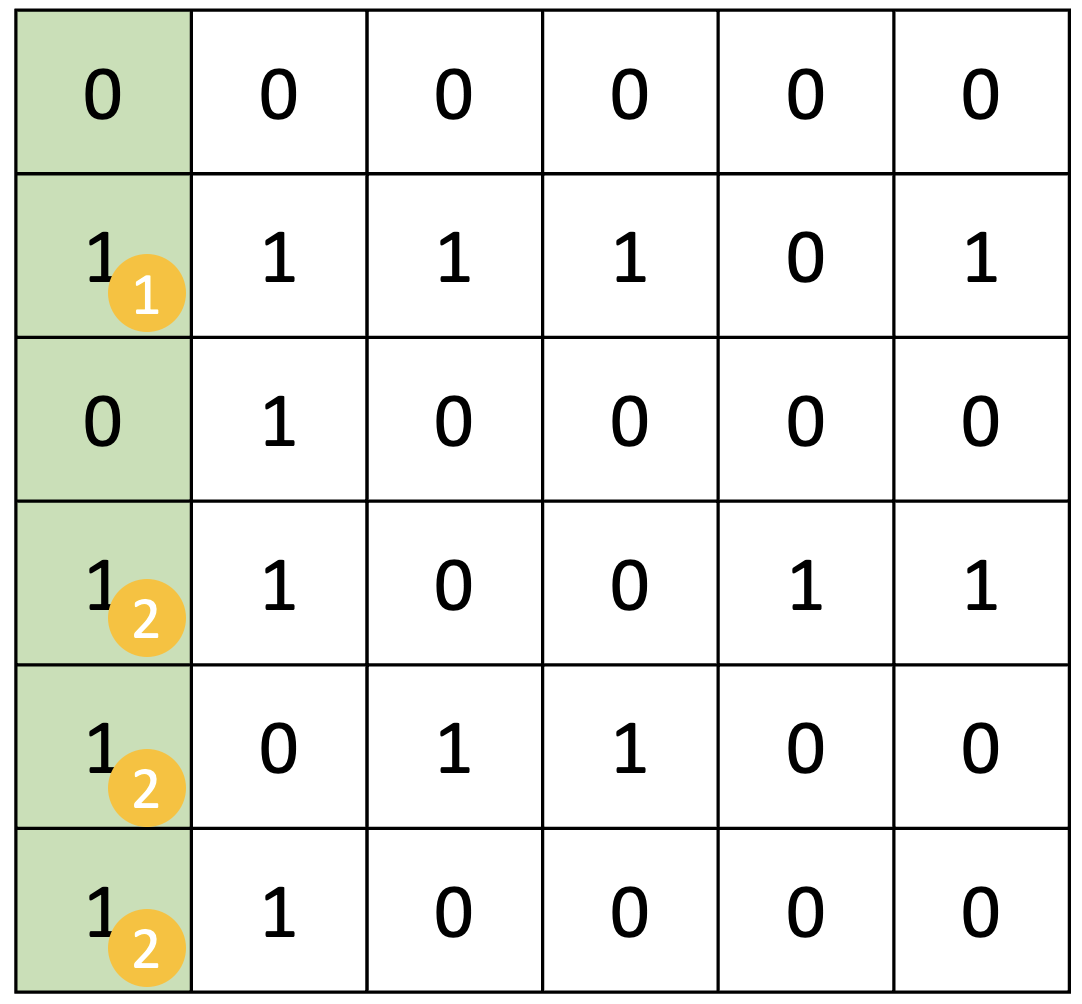구현 편의상 첫 행은 모두 0으로 채워진 패딩을 넣었다.
위 이미지는 0번째 열을 고려하는 상황이다. 이때 각 칸의 우측 아래 원은 집합 번호를 의미한다.
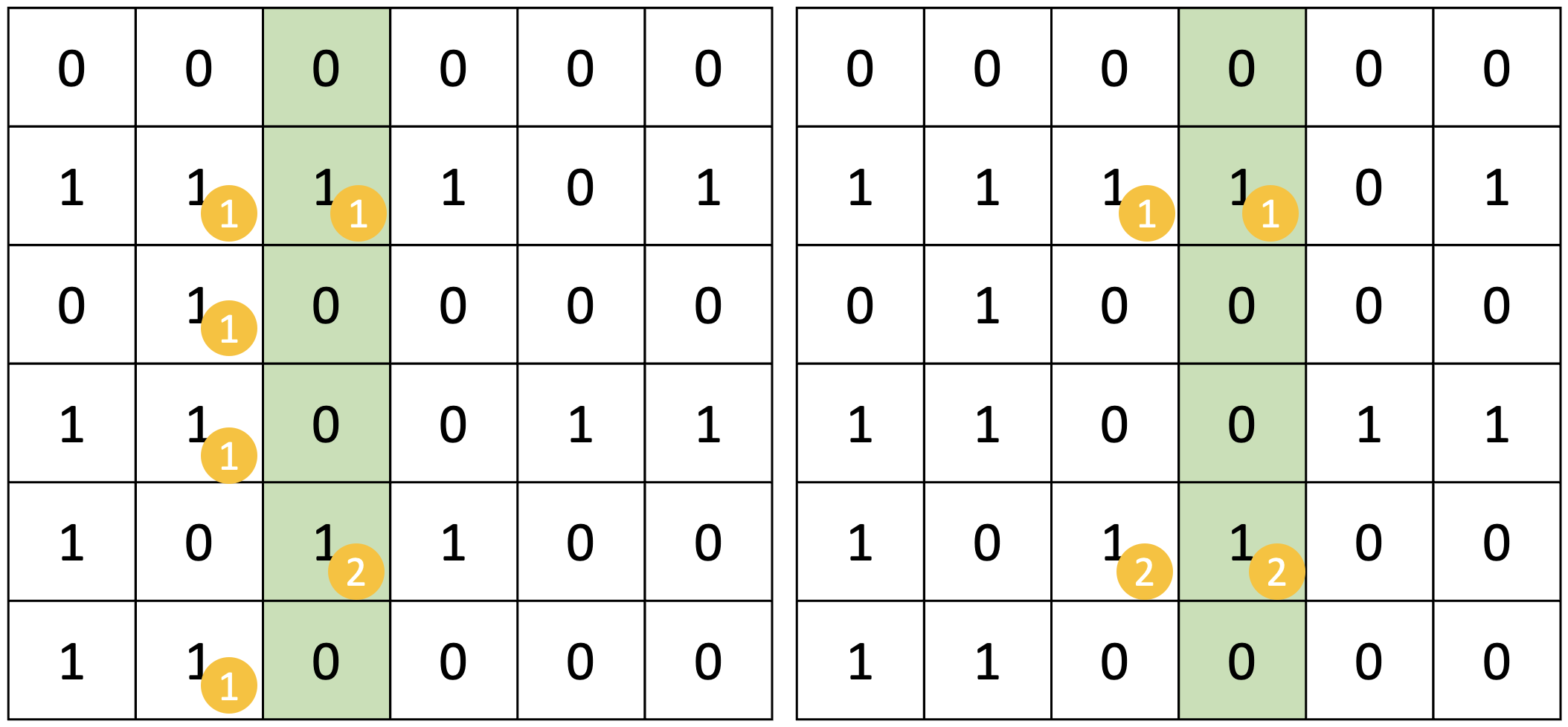
다음은 1번째 열을 고려하는 상황이다.
[3][1]을 보면 위쪽으로는 1번 집합, 왼쪽으로는 2번 집합이다. 따라서 1번과 2번 집합을 union 해준다.
[5][1]을 보면 왼쪽으로 2번 집합이지만, 1번과 union 된 상태이므로 더 작은 숫자인 1로 설정해준다.
이제 3번째 열을 고려할 차례이다.
우리는 1번 집합과 2번 집합을 union 하였다. 따라서 2번 집합은 더 이상 사용되지 않는다.
다음번 집합을 새로 할당해야 할 때, 우리는 2번 집합을 다시 사용해도 된다.
물론 이때는 1번 집합과 union 상태를 깨기 위해 parent[2]=2로 바꾸어야 한다.
1번 집합과 2번 집합이 union 상태라는 것은, 현재 고려하는 열이 끝날 때까지만 유지하면 된다.
이후에는 해당 집합 번호를 재사용해도 된다.
따라서 동시에 사용하는 집합 개수의 최댓값은 h개이다.
(왼) 3번째 열 고려, (오) 4번째 열 고려
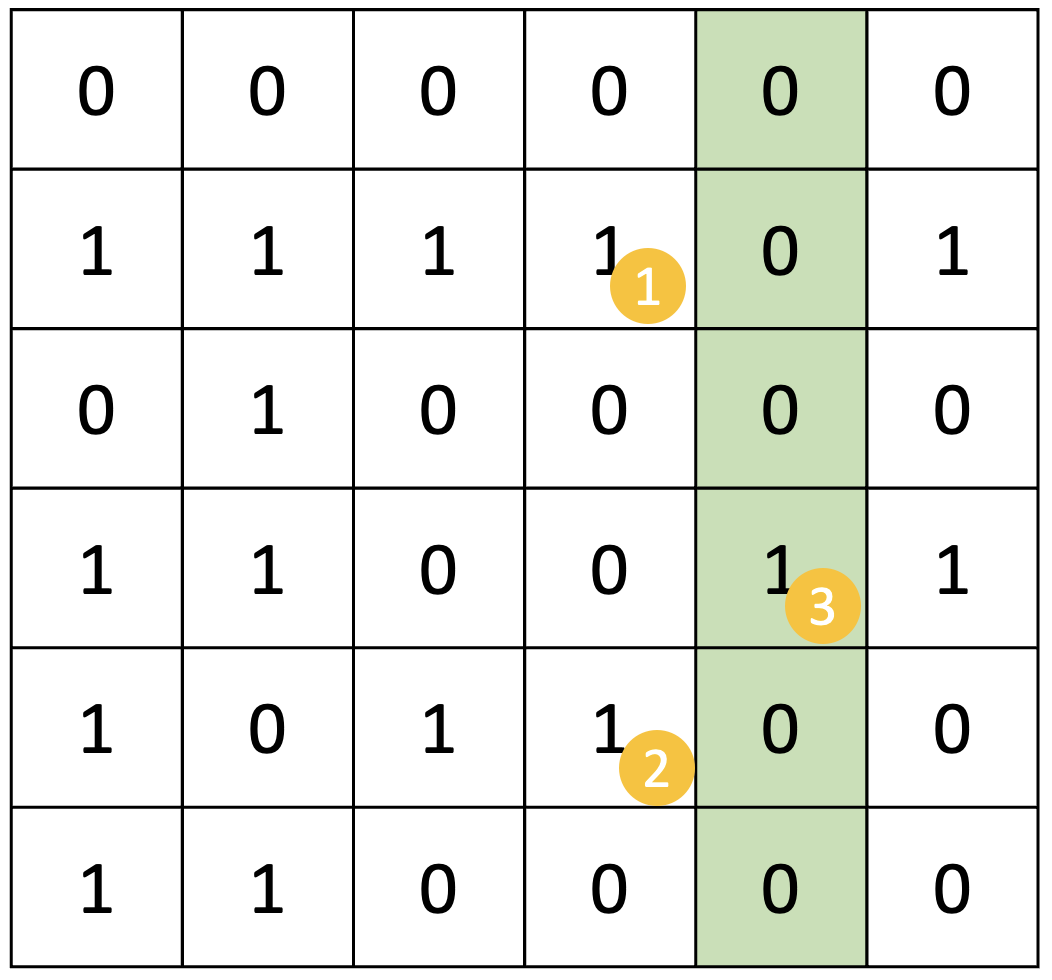
3번째, 4번째 열을 고려하는 상황이다.
직전 열보다 더 이전의 열들은 더 이상 고려하지 않아도 된다. 따라서 집합 번호를 모두 삭제해주었다. (헷갈리지 않기 위해)
(왼쪽 이미지에서)[4][2]가 2번 집합으로 새롭게 할당된 것을 볼 수 있다.
(나는 실제 구현 시 queue로 사용 가능한 집합 번호를 관리했기 때문에, 더 큰 수들이 먼저 할당되긴 한다.)
5번째 열 고려
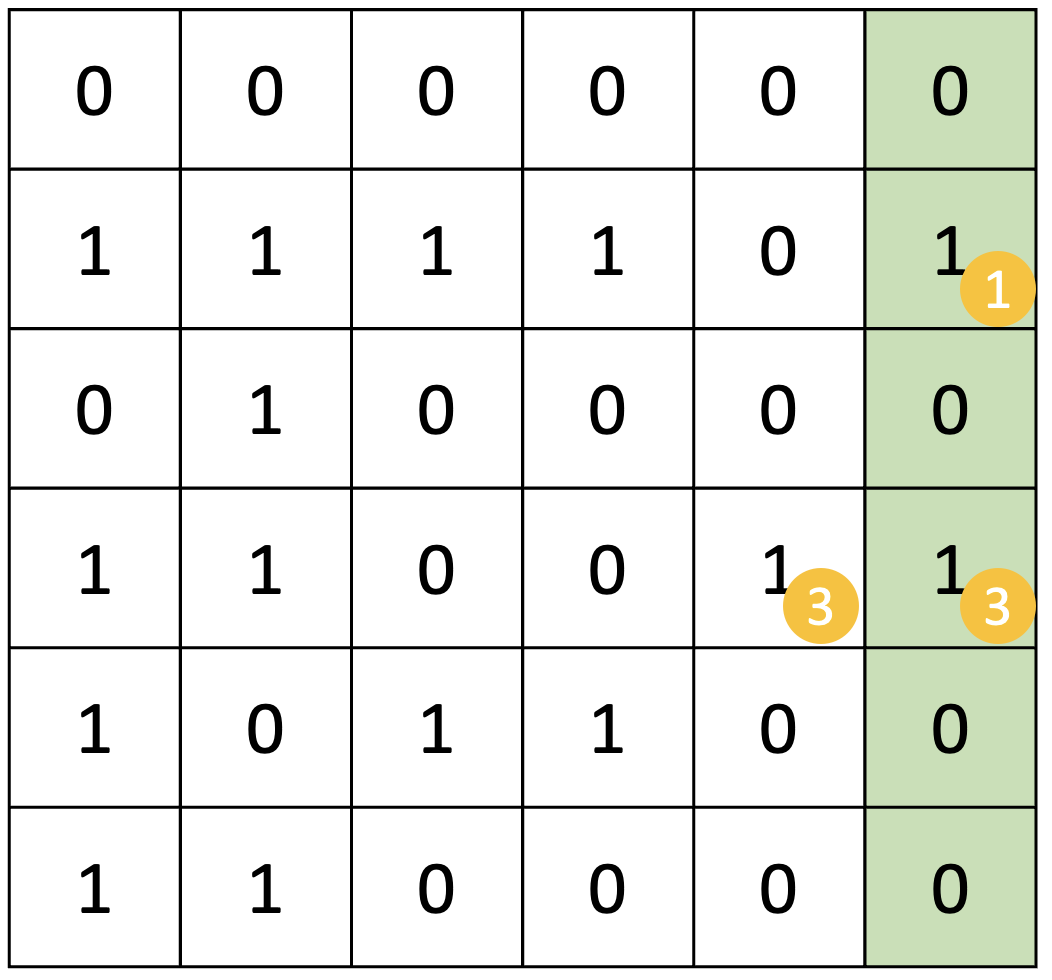
5번째 열을 고려하는 상황이다.
새로운 집합 번호인 3이 할당되었다.
또한 이제 1번, 2번 집합 번호는 유지할 필요가 없다. 필요하면 해당 번호를 사용해도 된다.
마지막 열 고려
이 외의 고려할 것들
0. 사용 가능한 집합 번호 관리
여러 방법이 있겠지만, 나는 Queue를 이용하여 관리하였다.
ispossible(ll mid) 함수 첫 부분에 Queue에 1번부터 h번까지 넣는다.
탐색 중 새로운 집합 번호가 필요하면 여기서 pop해서 사용하면 된다.
또한 merge 되거나, 직전 열에는 사용된 집합 번호지만 현재 열에서는 사용안된 집합 번호는 새롭게 Queue에 넣어준다.
y행에 할당된 집합 번호는 int setnumber[y]=집합번호를 사용했다.
2. 직전 열에는 사용된 집합 번호지만 현재 열에서는 사용안된 집합 번호란?
위와 같은 상황이다. 1번, 2번 집합은 더 이상 사용되지 않는다. 따라서 Queue에 넣어줘야 한다.
h개의 집합 번호가 모두 사용되는 케이스
이를 위해 int lastvisit[]와 int cnt를 사용했다.
새로운 열을 방문할 때마다 cnt++를 해주고, 현재 열에 사용된 집합 번호에 cnt를 할당해준다.
해당 열의 모든 행을 탐색한 뒤에 lastvisit[] 중에 cnt-1인 번호는 다시 Queue에 넣어준다.
1
2
3
4
5
6
void recycleSetnumber() {
// 해당 열의 마지막 칸까지 탐색한 뒤에 호출해준다.(즉, y==h일 때 호출해주자.)
// 직전 열에는 사용된 집합 번호지만, 현재 열에서는 사용안된 집합 번호
for (int i = 1; i <= h; ++i)
if (lastvisit[i] == cnt - 1) q.push(i);
}
3. 집합 크기는 어떻게 관리할 것인가.
우리는 최대 집합 크기가 mid개보다 작아야 한다. mid보다 커지면, 직전 열과 현재 열 사이에 칸막이를 놓고 모든 집합을 초기화 해야한다.
집합은 최대 h개이다. 집합 번호를 1번부터 h번까지 사용할 때, 집합 개수를 표현하는 1차원 배열을 사용하면 된다.
long long setsize[집합번호]={해당 집합의 원소 개수}
merge 시 집합 크기도 더해주는 것을 잊지 말자.
4. Union은 어떻게 구현할 것인가.
분리 집합 문제와 마찬가지로 parent[]을 사용한다. find() 함수도 사용한다.
또한 위에서 말했던 것처럼, 집합 사이즈도 합쳐줘야 한다.
5. 칸막이는 어떻게 구현할 것인가.
칸막이를 설치하게 되면, 모든 집합을 초기화시켜줘야 한다.
현재 집합 관리 queue를 모두 pop 해준 후, 다시 1번부터 h번까지 push해준다.
또한 주의해야 할 점은 칸막이 설치 직후(또는 첫번째 열)는 조금 특별하게 처리를 해주어야 한다.
예를 들어, 어떤 칸이 1이고 그 위쪽과 왼쪽이 모두 1이면, 왼쪽 집합과 위쪽 집합을 union 해야 한다.
하지만 칸막이 설치 직후나 첫 번째 열인 경우에는 왼쪽 열을 절대 고려하면 안 된다.
이를 위해 bool flag를 사용했다.
정리
이 문제는 아이디어보다는 구현하는 데 많은 시간이 필요했다. 위 내용만 봐도 고려해야 할 사항이 많다는 것을 알 수 있다.
제출된 코드들의 실행 시간, 메모리가 다양한 것을 봐서는 구현 방법도 여러 가지 있을 것 같다. 더 좋은 구현 아이디어가 있을지 고민해봐야겠다. 문제에 구현 태그도 달아줘요