KUPC 후기
2023년 11월 04일(토) 건국대학교 알고리즘 대회인 KUPC가 열렸습니다.
Alkon 동아리가 주최하여, SW 중심 대학과 STARTLINK, SOLVED.AC에서 많은 후원을 해주셨습니다.
60명이 넘는 학우분들이 참여해주셨고, 많은 스태프 도움으로 성공적으로 마무리되었습니다.
특히 동아리 회장의 압도적인 헌신으로 원활한 대회가 됐던 것 같네요.
저는 문제 테스터와 현장 스태프 역할을 했습니다.
사실 문제 출제자로 합류했으나 역량 부족 이슈가
대회 출제 목표 중 하나는 ‘어려운 알고리즘을 알지 못해도 풀리게 하자’ 였습니다.
예를 들어, 네트워크 플로우나 2-SAT 등을 사용하는 알고리즘은 최대한 지양했습니다.
그리고 그 목표를 잘 이루었다고 생각합니다. 테스터로 문제를 풀 때, 생각보다 높은 퀄리티에 감탄하면서 풀었던 것 같네요.
대회는 Division 1과 Division 2로 나누어서 진행됐습니다.
참가자들의 열기가 아주 뜨거웠는데, 11월임에도 에어컨을 틀 정도였습니다.
특히 생각보다 전반적으로 높은 성적이 나와서 놀랐습니다.
이번 대회는 백준 대회와 solved.ac 아레나에도 등록됐습니다.
백준 대회에는 400명이, 아레나에는 330명이 참가해주셨습니다.
교내 대회를 목표로 출제한 문제들이라 그런지, 올솔브가 무려 10분입니다.
초간단 문제 해설
곧 공식 에토리얼이 올라오는 것으로 알고있는데, 그 전에 간단한 풀이를 올리겠습니다.
solved.ac에 공식 해설이 업로드됐습니다.
A. 얼룩말을 찾아라
연속된 \(1\)의 집합을 카운트하면 되는 문제였습니다. For문을 한번만 돌리면 되므로 \(O(NL)\)에 풀 수 있습니다.
B. 이제는 더 이상 물러날 곳이 없다.
게임 이론 문제였지만, 주어진 예제로 인해 규칙을 쉽게 발견할 수 있습니다. 건덕이와 건구스 사이의 칸이 홀수인지 짝수인지만 판별하는 문제였습니다. 길이가 달라도 홀짝의 규칙은 변하지 않기 때문에 입력이 홀수면 Goose, 짝수면 Duck을 출력하면 됩니다. \(O(1)\)에 풀립니다.
C. 바닥수
곱셈의 항등원인 \(1\)을 이용하는 문제입니다. 앞부분의 \((l-1)\)개를 \(1\)로 채우고, 마지막 \(l\)번째만 입력으로 들어온 수로 채우면 됩니다. \(O(L)\)에 풀립니다.
D. 단체줄넘기
키가 가장 큰 사람이 가운데 부분이 위치하면 됩니다. 양쪽 방향으로 그리디하게 세울 수 있으면 세우면 됩니다.
먼저 내림차순으로 정렬합니다. 그리고 left, right로 나누어서 계산하면 됩니다.
더 쉬운 생각으로는, 같은 키를 가진 사람은 최대 2명만 세울 수 있습니다. 따라서 같은 키를 가진 사람 수를 카운트하고 ans += min(2, arr[i]) 을 계산하면 됩니다. \(O(N)\)에 풀립니다.
E. 팰린드롬 애너그램
왼쪽과 오른쪽 문자를 횟수 제한 없이 위치를 바꿀 수 있습니다. 따라서 모든 경우가 가능합니다. 각 문자의 개수가 모두 짝수개면 됩니다. 이때 입력 문자열 길이가 홀수이면 가운데 문자는 빼줍니다. \(O(N)\)에 풀립니다.
F. 현수막 걸기
이분 탐색을 이용하는 문제입니다. 가능한 말뚝 거리를 모두 구한 뒤 정렬합니다. 이제 깃대를 기준으로 For문 돌리면서 \((깃대*말뚝거리/2)<=R\)을 만족하는 최대 말뚝거리를 이분탐색으로 구하면 됩니다. \(O(N^2+M\log N)\)에 풀립니다.
G. 스위치
DP를 이용하는 문제입니다. ‘dp[i]=i초에 얻을 수 있는 최대 점수’를 사용하면 됩니다. \(O(N)\)에 풀립니다.
H. 낚시
부분합과 DP를 이용하는 문제입니다. 어떤 위치에서 수면 위까지의 물고기 합은 부분합으로 미리 구해줍니다. 이후 계단 모양으로 왼쪽으로 이동하며 더하면 됩니다. Q의 제한이 크므로 2차원 배열에 값을 저장해놓고, 나중에 필요하면 꺼내쓰면 됩니다.
I. 시간낭비
DP 또는 DAG 그래프를 이용해서 풀 수 있습니다. 방향전환이 최대 2번이므로 가능한 방향은 오른쪽, 왼쪽, 오른쪽입니다.
또한 ‘최초로 도착’하는 최대 시간이기 때문에 예외처리를 해주어야합니다. 등굣길을 벗어나는 경우와 이동가능 수가 0인 경우도 예외처리 해주어야 합니다.
풀이 1. DP
‘dp[i]=i번에 도착할 수 있는 최대 시간’으로 정의합니다. 이후 for문을 3번 돌리는데, 각각 오른쪽, 왼쪽, 오른쪽 방향입니다. 예를 들어 오른쪽 방향인 경우 dp[i + arr[i]] = max(dp[i + arr[i]], dp[i] + 1), 왼쪽 방향인 경우 dp[i - arr[i]] = max(dp[i - arr[i]], dp[i] + 1)를 사용하면 됩니다.
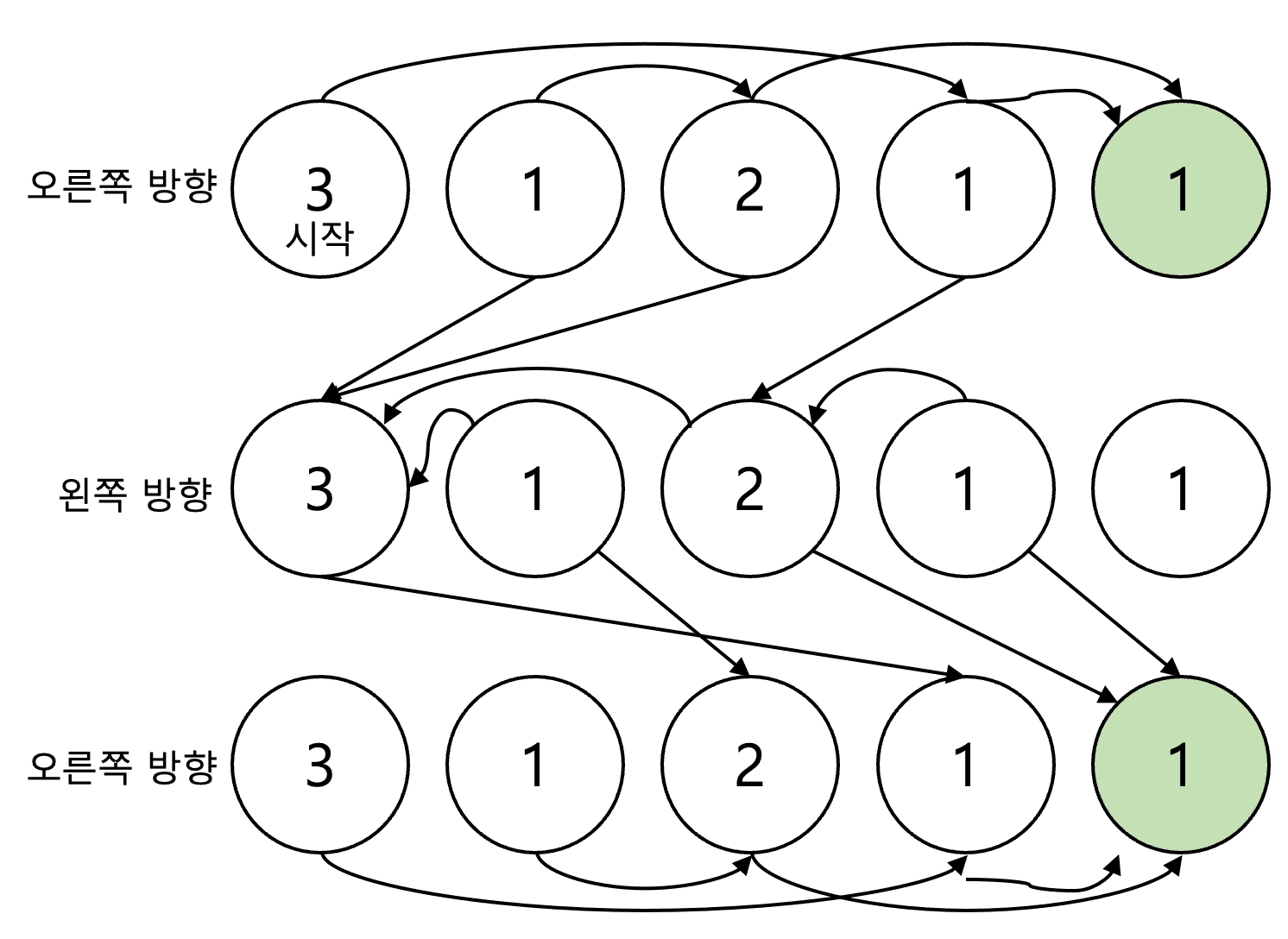
풀이 2. DAG
DAG는 아래와 같이 그래프를 디자인하면 사이클이 없는 방향그래프(DAG)를 만들 수 있습니다. DAG의 경우 위상정렬을 이용하면 최장거리를 구할 수 있습니다. 아래 코드를 참고해주세요.
DAG의 경우 이분 풀이인데, 참 놀랍네요.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void sort() {
queue<int> q;
for (int i = 0; i < 3 * n; ++i) {
if (indegree[i] == 0) q.push(i);
}
int here;
while (!q.empty()) {
here = q.front();
q.pop();
for (int i = 0; i < edge[here].size(); ++i) {
int there = edge[here][i];
indegree[there] -= 1;
if (indegree[there] == 0) q.push(there);
if (dist[here] != -1)
dist[there] = max(dist[there], dist[here] + 1);
}
}
}
K번부터는 다음 게시물에서 업로드하겠습니다.