KUPC 해설2

대회 링크, 공식 해설

A번부터 I번까지의 문제 해설은 이전 게시물을 참고해주세요.
K번 문제부터 난이도가 어렵습니다. 천천히 살펴보도록 하죠

K. MEXchange

주어진 수열 $B$는 반드시 오름차순이어야 합니다. 그리고 마지막 원소는 반드시 $n+1$이어야합니다. 만일 그렇지 않다면 No를 출력하시면 됩니다. 이 규칙은 금방 찾았으리라 생각됩니다.
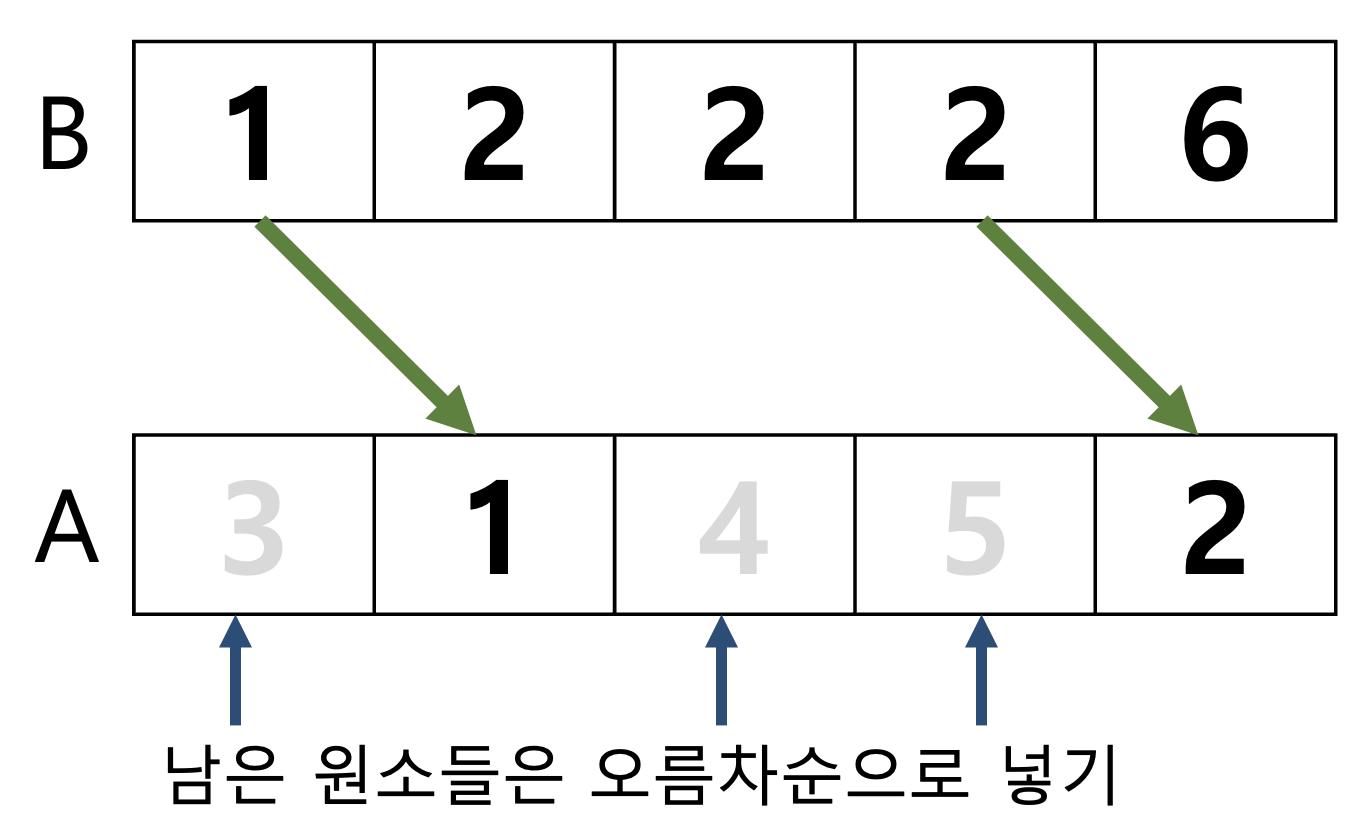
수열 $B$에서 수가 바뀌는 순간을 생각해볼께요. 예를 들어, $1, 2, 2, 2, 6$이라 하겠습니다. 2에서 6으로 바뀌는 이유가 뭘까요? 바뀌는 순간에 순열 $A$에서 해당 수가 등장했기 때문입니다. 따라서 순열 $A$는 (X, X, X, X, 2)와 같은 모양이어야만 합니다. 1에서 2로 바뀌는 순간도 마찬가지입니다. 결론적으로 이 규칙을 통해 우리는 순열 $A$가 (X, 1, X, X, 2)라는 것을 알 수 있습니다.
이제 나머지 X 부분도 채워보죠. 이 문제는 스페셜 저지 입니다. 따라서 답이 여러개 나올 수 있어요. (답이 가능하다면) 무조건 가능한 경우는, X 부분에 남은 수들을 오름차순으로 그리디하게 수를 채우면 됩니다. 왜그럴까요?
주어진 수열 $B$는 오름차순이어야만 합니다. 또한 반드시 $i$번째 원소인 $B_i$는 $A_j < B_i, \forall j>i$이어야 합니다. 따라서 답이 존재한다면 위와 같은 전략으로 만든 $A$가 반드시 존재합니다.
$A$를 찾은 뒤 다시 한번 for문을 돌리면서 주어진 $B$를 만족하는지 체크해줍니다. 만족하지 않다면 No를, 만족한다면 Yes와 $A$를 출력하시면 됩니다. $O(N)$에 풀 수 있습니다. 당장 이해가 안되더라도, 펜으로 따라가시면서 천천히 생각해보시면 금방 이해되실 겁니다.

L. 등불 날리기

사이즈가 S인 구간에서 $i<j, A_i < A_j$ 인 pair의 개수를 구하는 문제였습니다. inversion count라는 알고리즘이 존재합니다. 궁금하신 분은 직접 찾아보시면 좋을것 같습니다.
다른 방법으로는 슬라이딩 윈도우 + 세그트리 + 좌표압축으로 풀 수 있습니다. 아이디어가 아주 기발한데, 아마 전에 접해보지 않았다면 상당히 어려울 것 같습니다. 저도 이전에 어느 문제에서 이 아이디어를 본 적이 있는데, 완전히 잊고 있다가 무척 힘들게 풀었네요.
먼저 쉬운 이해를 위해 가정을 하겠습니다. 사이즈가 S인 어떤 구간은 주어진 배열 $A$의 적절한 중간에 위치해있고, 찾고자 하는 pair의 개수를 알고있다고 하겠습니다.

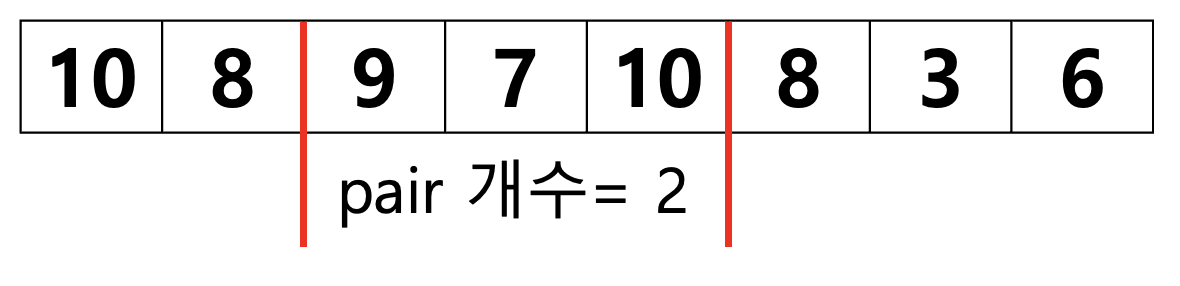
구간을 오른쪽으로 한칸 이동하고 싶습니다. 즉, 9를 내보내고 8을 포함시키고 싶습니다. 그럼 pair의 개수 변화는 어떨까요? 9로 인해 추가된 pair개수는 빼야합니다. 그리고 새로 들어온 8로 인해 추가된 pair 개수는 더해야 합니다. 이때 사용하는 아이디어가 세그트리입니다.
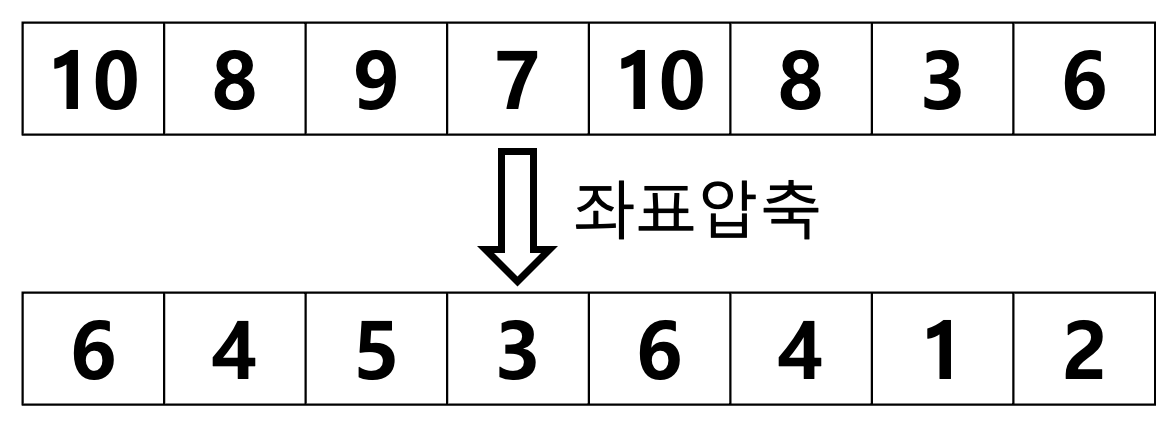
먼저 좌표압축을 하겠습니다. 모든 원소를 오름차순 정렬 후 1부터 숫자를 쭉 부여하겠습니다. 이때 같은 수를 가지면 압축도 같은 수로 해야합니다. 우리는 수들의 대소관계만 유지하면 되기 때문에 본질적인 문제는 바뀌지 않습니다. 좌표 압축 후에 최소는 1, 최대는 M이라 하겠습니다.

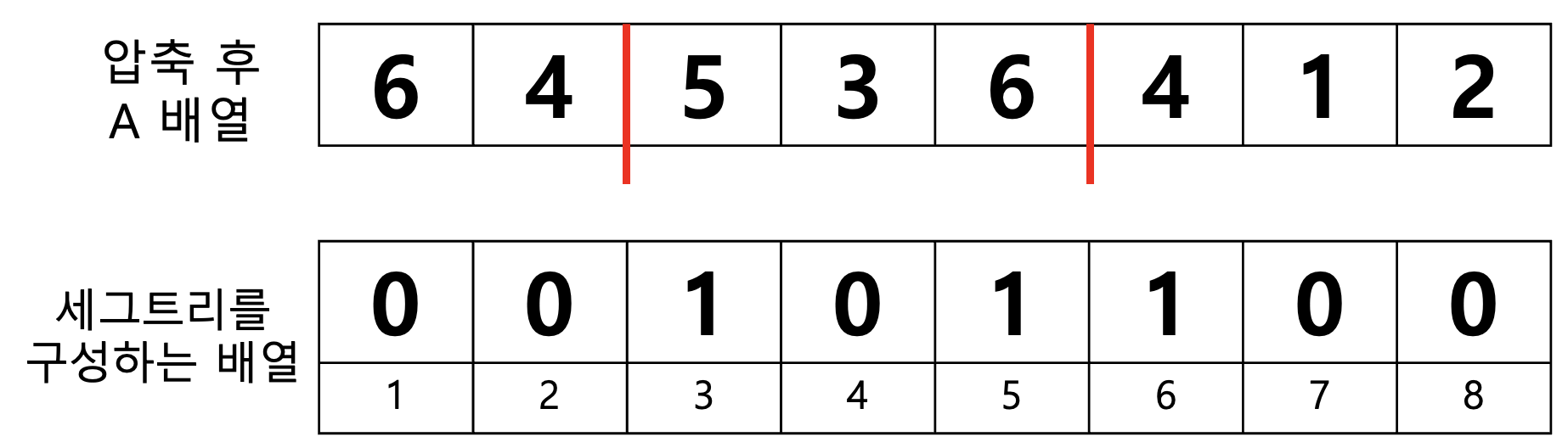
세그트리를 사용하면 구간 6부터 M까지의 원소 합을 구할 수 있는데요, 이를 활용해서 원소 개수를 카운팅해주면 됩니다.

우리는 5를 내보내고 싶습니다. 따라서 6이상, M이하의 원소 개수를 pair에서 빼야해요. 즉, 세그트리에서 find(6, M)을 pair에서 빼주면 됩니다. 그리고 세그트리를 업데이트해줍니다. (인덱스 5번원소를 -1 시키기 : update(5, -1))
그리고 우리는 4를 추가하고 싶습니다. 세그트리에서 find(1, 3)을 pair에 더한 뒤 세그트리를 업데이트 해줍니다. (update(4, +1))

위 과정을 슬라이딩 윈도우를 이용해 오른쪽으로 쭉 이동시키며 반복하면 됩니다. 세그먼트 트리 연산이 $O(\log N)$이므로 총 시간복잡도는 $O(N\log N)$ 입니다.

M. 우정은 BFS처럼, 사랑은 DFS처럼

수식으로 증명하기 까다로운 문제입니다. 아마 대회 중에는 Proof by AC로 푸신 분들이 많은 것 같습니다. 손으로 몇 개의 그래프를 그리다보면 대충 이런 모양이겠거니~ 하는 감이 오는데, 이를 정확하게 증명하기 쉽지 않네요. 추후 업데이트 하겠습니다. 대신 공식해설을 참고해주세요.

N. 양손 정렬

문제는 공식 해설을 참고해서 만들었습니다. 두 변수의 값을 서로 바꾸는 swap은 아래와 같이 tmp 변수를 이용합니다. 저희는 이 개념을 적극 사용할 예정입니다.

void swap(int &a, int &b) {
  int tmp = a;
  a = b;
  b = tmp;
}

배열의 ‘파티션’을 정의하겠습니다. 왼쪽 $\lfloor n/2 \rfloor$ 개는 LEFT, 오른쪽 $\lfloor n/2 \rfloor$ 개는 RIGHT라 하겠습니다.
우리는 배열의 모든 원소들을 서로 자리바꿈할 수 있습니다. swap을 생각해보세요. 서로 교환되어야 할 원소의 파티션이 같다면, 반대편 파티션의 원소를 tmp로 사용해서 3번의 교환으로 자리바꿈 할 수 있습니다. 서로 바꿔야하는 원소들의 파티션이 다르다면 1번의 교환으로 자리바꿈이 가능합니다. 하지만 배열의 사이즈가 홀수일 때 정가운데는 자리바꿈이 불가능하므로, n is odd && A[(n+1)/2]!=(n+1)/2의 경우만 -1을 출력하면 됩니다.

이제 아주 신기한 아이디어가 나옵니다. 사실상 이 아이디어 때문에 티어가 높은 것 같습니다.
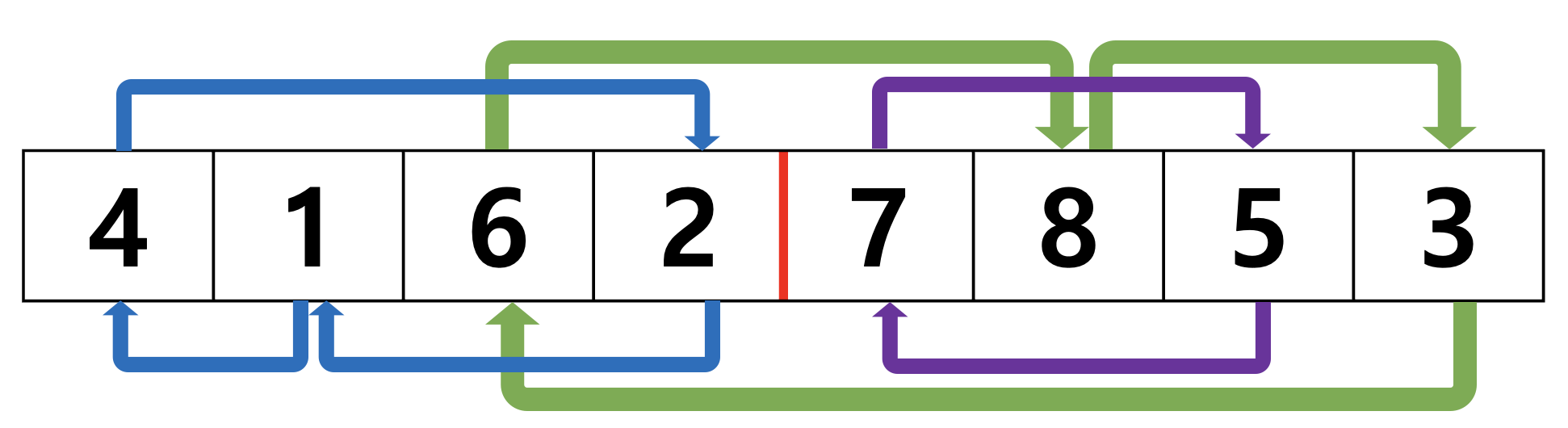
배열에서 각 원소가 목표하는 자신의 자리를 가르키는 엣지를 나타내면 아래와 같습니다. 예시 배열은 [4, 1, 6, 2, 7, 8, 5, 3]을 사용하겠습니다.

위 그림에서 3개의 사이클을 확인할 수 있습니다. 나타날 수 있는 사이클의 종류는 총 3가지입니다.

1. 왼쪽 파티션으로만 이루어진 사이클(파랑색)
2. 오른쪽 파티션으로만 이루어진 사이클(보라색)
3. 두 파티션을 모두 사용하는 사이클(초록색)

먼저 3번에 해당하는 초록색 사이클을 살펴보겠습니다. 만일 두 파티션을 모두 사용하는 사이클의 원소 개수가 n이라면 n-1번의 교환으로 올바르게 배치시킬 수 있습니다. 마치 swap에서 tmp 변수를 사용하는 것을 떠올리시면 됩니다.

특징 1. 두 파티션을 모두 사용하는 사이클은 $n-1$번의 교환으로 배치시킬 수 있다. ($n$ is cycle size)

이제 왼쪽 파티션으로만 이루어진 사이클을 보겠습니다. 이 경우 오른쪽 파티션에 있는 아무 원소 하나를 잡고 사이클의 아무 원소와 자리를 바꾸면 어떻게 될까요? 3번 사이클인 ‘두 파티션을 모두 사용하는 사이클’로 바뀝니다.
예를 들어 (4, 2, 1)로 이루어진 사이클에서 1과 8의 자리를 바꾸면 (4, 2, 1, 8)로 이루어진 사이클이 되고, 이는 3번에 해당하는 사이클입니다. 이것은 오른쪽 파티션으로만 이루어진 사이클도 동등하므로 다음과 같이 정리할 수 있습니다.

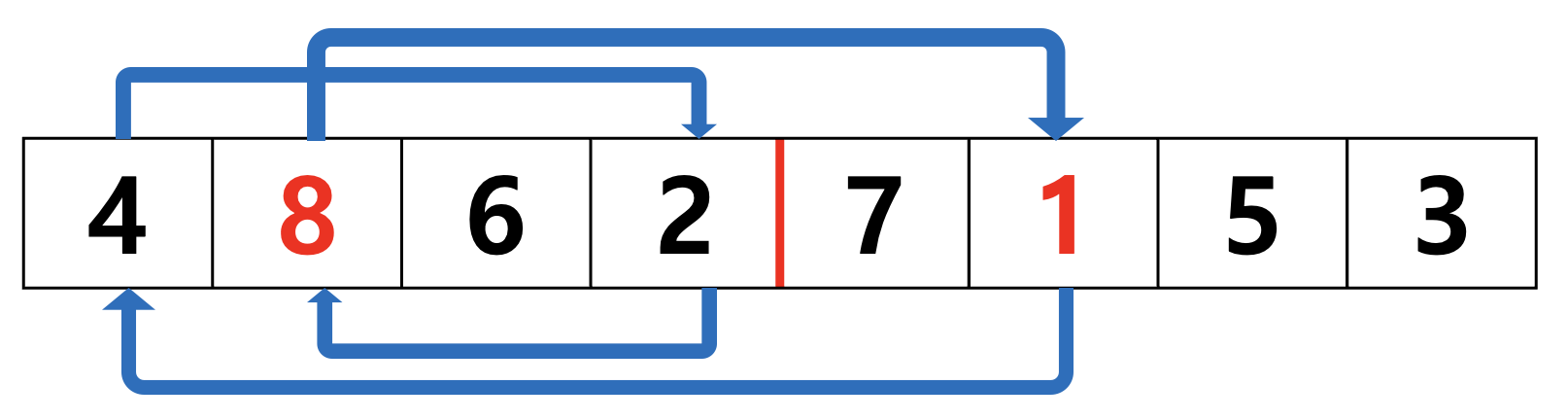이때 8은 원래 있던 자리를 가르키게합니다. 즉, 원상복구 시키는 자리입니다..

특징 2. 한쪽 파티션만 사용하는 사이클은 1번의 교환으로 $n+1$개로 이루어진 3번 사이클로 변환할 수 있다. ($n$ is cycle size)

마지막으로 하나의 특징을 더 보겠습니다. (4, 2, 1) 사이클을 3번 사이클로 변환시키고 싶습니다. 오른쪽 파티션에 속한 아무 원소나 잡고 교환시키면 3번 사이클이 됩니다(특징 2). 근데 ‘아무 원소’ 말고, 오른쪽 파티션으로만 이루어진 사이클의 원소와 교환시키면 어떻게 되나요? 두 사이클이 자연스럽게 섞이면서 3번 사이클로 바뀝니다.
예를 들어, 2과 7을 교환시키겠습니다. 그럼 (4, 1, 2), (7, 5) 사이클이 자연스럽게 하나의 3번 사이클로 만들어집니다.

특징 3. 1번 사이클($a$ size)과 2번 사이클($b$ size)은 1번의 교환으로 $a+b$개로 이루어진 3번 사이클로 변환할 수 있다.

위 3개의 특징을 이용하면 문제를 풀 수 있습니다. 모든 사이클은 3번 사이클로 변환시켜야합니다. 1번 사이클과 2번 사이클을 최대한 섞는 전략을 사용해야 합니다(특징 3). 두 사이클의 개수가 같지 않다면 어쩔 수 없이 (특징 2)를 이용합니다. 그리고 최종적으로 (특징 1)을 이용해 답을 구합니다.