Diffie-Hellman, ElGamal

RSA, Diffie-Hellman, ElGamal은 공개키 암호 시스템 자체로도 사용되지만, 대칭키 암호 시스템에서 키 교환을 위해서도 많이 사용됩니다.
특히 최근 TLS에서는 타원곡선을 이용한 Diffie-Hellman(ECDHE)를 많이 사용합니다.

Discrete Log Problem

Generator

if $Z_n^{*}=\lbrace g, g^2, \dots, g^{\varphi(n)}(=1)\rbrace$, then $g$ is a Generator of $Z_n^{*}$

예를 들어, $n=7$이라면 $Z_n^{*}=\lbrace 1, 2, 3, 4, 5, 6\rbrace$이다. $3^1=3, 3^2=2, 3^3=6, 3^4=4, 3^5=5, 3^6=1 \mod 7$ 이므로 $3$은 $Z_7^{*}$의 Generator이다.
추가) $Z_n^{*}$ contains a Generator $\iff n=1, 2^2, p^k, 2p^k$ where $p$ is an odd Prime (증명생략)

Discrete Log Theorem

If $g$ is a generator of $Z_n^{*}$, then the equation $g^x ≡ g^y \mod n$ holds if and only if the equation $x ≡ y \mod φ(n)$ holds

Discrete Log Problem

Given $n, g, x$, find $k$ such that $g^k=x \mod n$

여기서 $n$이 소수이고, $g$이 $Z_n^{*}$의 generator라면 $g^1, g^2, g^3, \dots, g^{n-1}$은 모두 다른 값이 된다. 따라서 식을 만족하는 $k$를 찾기 매우 힘듦.

한쪽은 계산하기 어렵고, 반대 방향은 계산하기 쉬운 함수를 one-way function이라고 한다.
DL Problem에서 $n, g, k$가 주어지면 $x$를 찾는 건 쉽지만, $n, g, x$가 주어질 때 $k$를 찾는건 어렵다.
DL Problem은 $NP \cap co-NP$ 문제로 알려져있다.

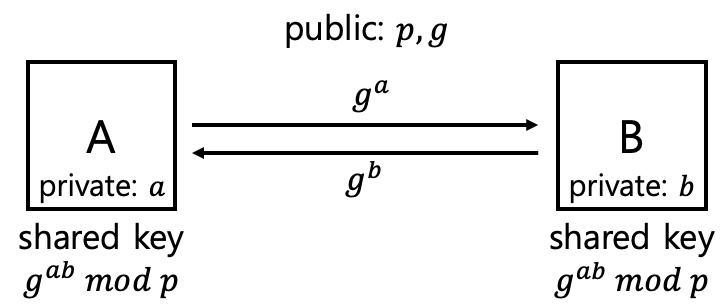
Diffie-Hellman Key Exchange

• 대칭키시스템에서 사용할 key를 생성하는 과정

• Setting
  • public : $p, g$
    • $p$ is prime
    • $g$ is generator of $Z_p^{*}$
  • Alice’s Public Info: $g^a \mod p$
  • Alice’s Secret Info: $a(<p)$
  • Bob’s Public Info: $g^b \mod p$
  • Bob’s Secret Info: $b(<p)$
• Shared Key Generation
  • Alice computes : $(g^b)^a = g^{ab} \mod p$
  • Bob computes : $(g^a)^b = g^{ab} \mod p$
• 안전할까?
  • $g^a$에서 $a$를 알아내는건 DL 문제
  • $g^a, g^b$로부터 $g^{ab}$를 알아낼 수 있을까?
    • Computational Diffie-Hellman Problem

ElGamal

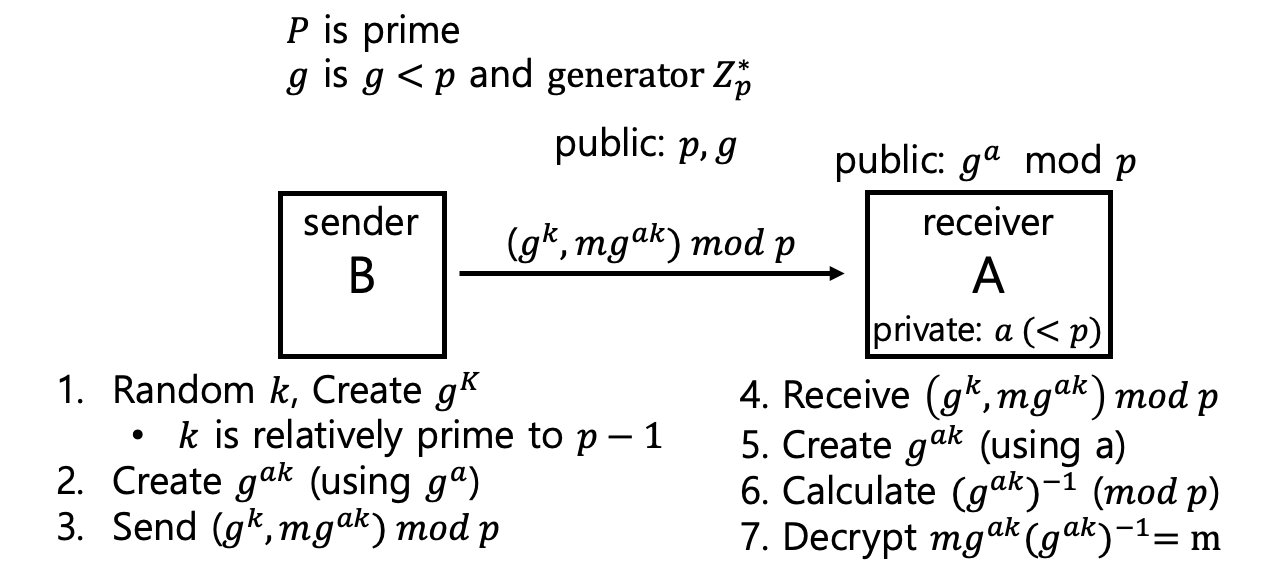
Setting

• public : $p, g$
  • $p$ is prime
  • $g$ is generator of $Z_p^{*}$ and $g \in Z_p^{*}$
• Alice’s Public Info: $g^a \mod p$
• Alice’s Secret Info: $a(<p)$

ElGamal Send Message $𝑚$

• Sender computes:
  • Random $k$
    • $k$ is relatively prime to $p-1$
  • Send $(g^k \mod p, mg^{ak} \mod p)$
• Receiver computes:
  • Create $(g^k)^a=g^{ak} \mod p$
    • $A$는 $a$를 가지고 있으므로 계산할 수 있다.
  • Calculate $(g^{ak})^{-1} \mod p$
  • Decryption: $mg^{ak}(g^{ak})^{-1}=m \mod p$