이분 매칭(Bipartite Matching)

N명의 사람이 M개의 일을 처리해야 한다. 각 사람은 최대 1개의 일만 할 수 있고, 각 일(job)도 최대 1명만 담당할 수 있다. 최대한 많은 일을 처리하려면 어떻게 해야 할까?

이때 사용하는 알고리즘이 이분 매칭이다.

이분 그래프(Bipartitle Graph)

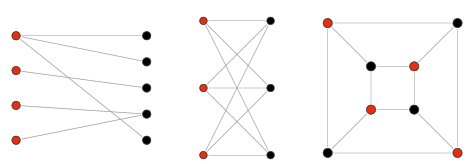
이분 그래프란 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프이다.
다시 말해, 그래프의 모든 정점이 두 그룹으로 나눠지고, 서로 다른 그룹의 정점이 간선으로 연결돼 있는 그래프를 의미한다.

이분 매칭(Bipartite Matching)

이분 그래프에서 각 정점이 다른 그룹과 연결되어 있는 간선을 최대 1개만 갖도록 구성하는 것을 이분 매칭이라고 한다.
물론 이분 그래프이므로 같은 그룹 내에서는 간선이 존재하면 안된다.
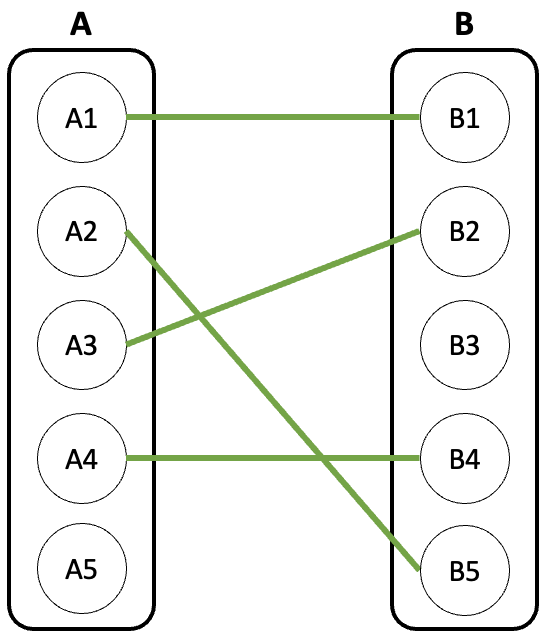
예를 들어 아래와 같은 구성을 이야기한다.

우리의 목표는 이분 그래프에서 최대한 많은 매칭(최대 간선 수)을 하는 것이다.

이분 매칭 과정

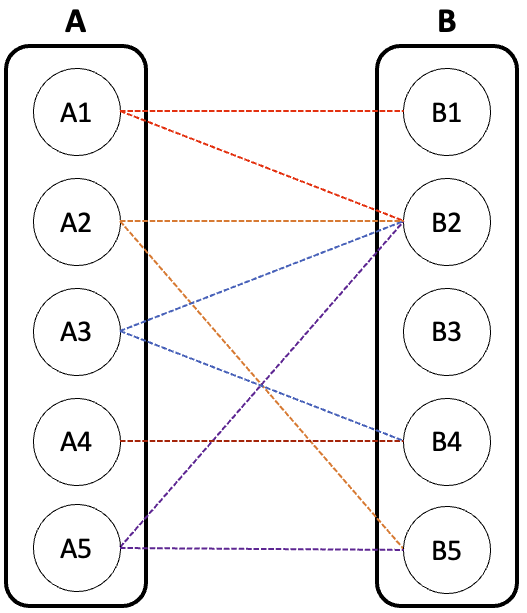
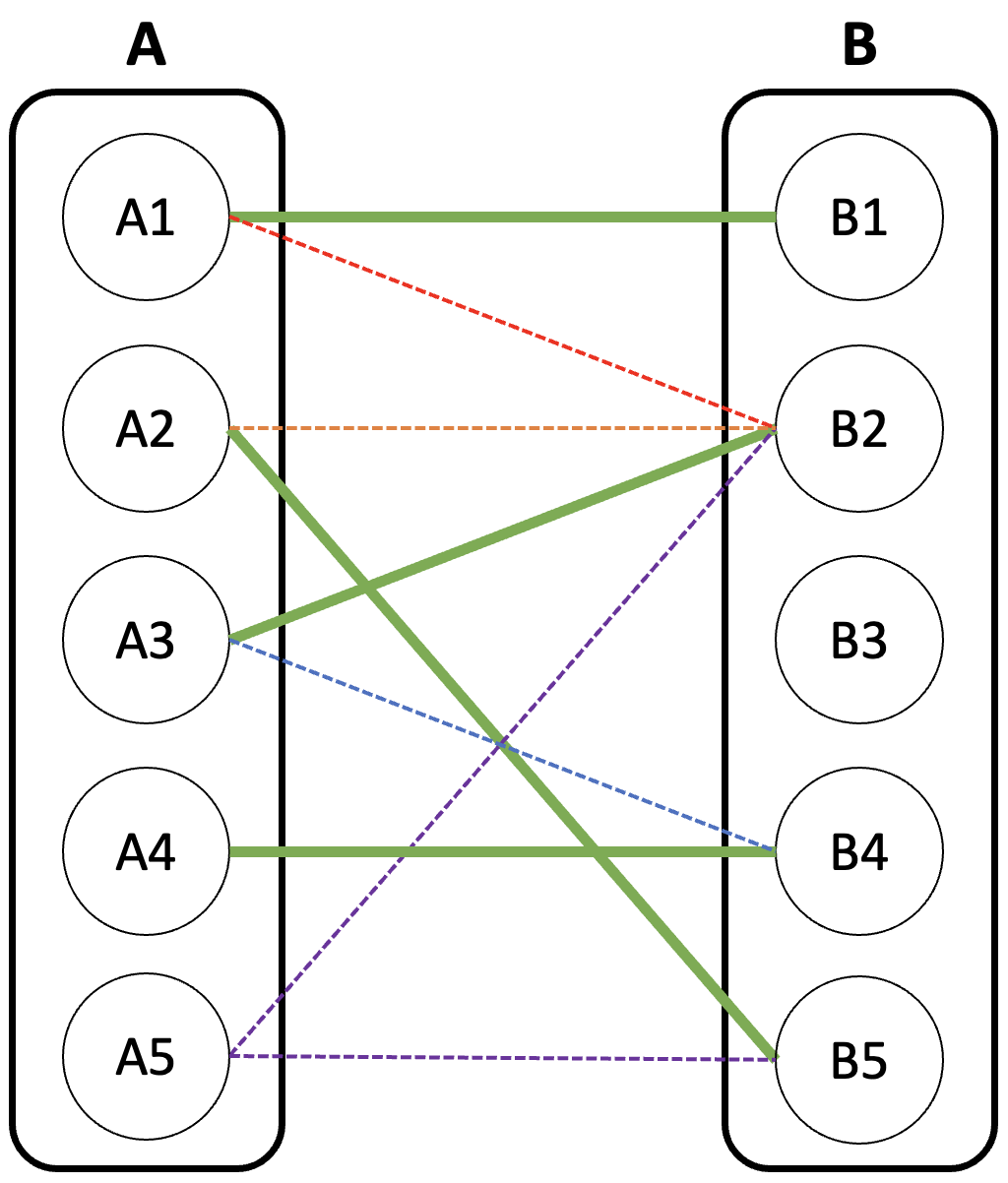
먼저 아래와 같이 이분 그래프가 존재한다고 가정하자.

A그룹을 기준으로 생각해보자.
먼저 A1은 B1 또는 B2에 연결할 수 있다. 두 노드 모두 아직 매칭이 안 됐으므로 어느 것을 선택해도 상관없지만, 위쪽 간선이 우선순위가 높다고 가정하자. 그럼 A1은 B1에 연결하게 된다.
마찬가지로 A2는 B2와 매칭시킬 수 있다.

A1과 A2를 매칭시킨 모습

이제 A3를 매칭시켜보자. A3는 B2 또는 B4와 연결할 수 있다.
하지만 B2는 이미 다른 노드(A2)에 의해 매칭이 되어 있다.
그럼 다시 A2로 돌아와서 다른 노드와 연결을 시도하게 된다.
A2가 연결 가능한 노드인 B5는 아직 매칭되지 않았음으로 A2는 B5와 연결하게 된다.
이제 B2는 매칭이 되어 있지 않으므로, A3는 B2와 연결한다.

Q: 그냥 A3가 B4와 연결하면 충돌 없이 매칭시킬 수 있지 않나?
A: 그렇게 Greedy하게 연결하면 최대 매칭을 하지 못한다. 이는 조금만 생각해보면 반례를 떠올릴 수 있다.

A4는 B4와 연결할 수 있는데, B4는 아직 매칭이 안 됐으므로 두 노드를 연결한다.

A2 매칭 수정, A3와 A4를 새롭게 매칭

이제 A5를 매칭시켜보자. A5는 B2 또는 B5와 연결을 할 수 있다.

• 먼저 B2와 연결을 시도하자.
  • B2는 이미 A3에 의해 매칭되었다.
  • A3가 B2 말고 다른 노드와 연결할 수 있을까?
  • A3가 B4와 매칭을 할 수 있는지 시도하자.
    • B4는 이미 A4에 의해 매칭되었다.
    • A4가 B4 말고 다른 노드와 연결할 수 있을까?
      • 없다.
  • 따라서 A5는 B2와 연결하지 못한다.
• 그럼 B5와 연결을 시도하자.
  • B5는 이미 A2에 의해 매칭되었다.
  • A2가 B5 말고 다른 노드와 연결할 수 있을까?
  • A2가 B2와 매칭을 할 수 있는지 시도하자.
    
    • B2는 이미 위에서 시도했었던 노드이다.(A5와 B2를 매칭 시도했었음)
    • 그럼 또 방문해서 조사할 필요가 없다. 어차피 실패할 것은 분명하기 때문이다.
      
  • 따라서 A5는 B5와 연결하지 못한다.
    

현재 진행 중인 DFS에서 이미 방문했던 노드를 방문하게 되면 더 깊이 탐색할 필요 없다.
이런 확인 없이 DFS를 계속 진행하게 되면 무한 재귀에 빠지게 된다.

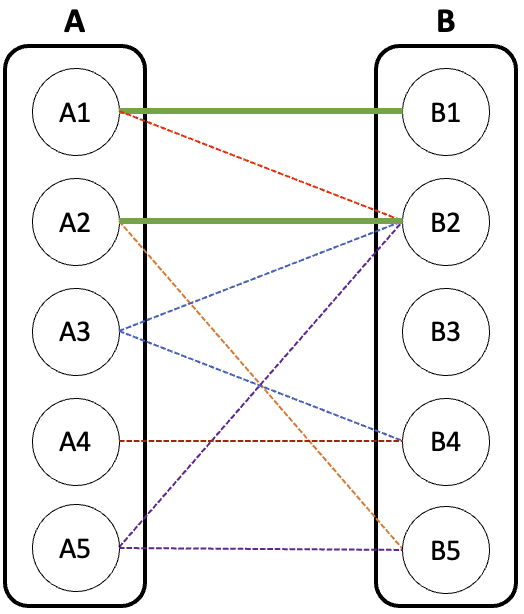
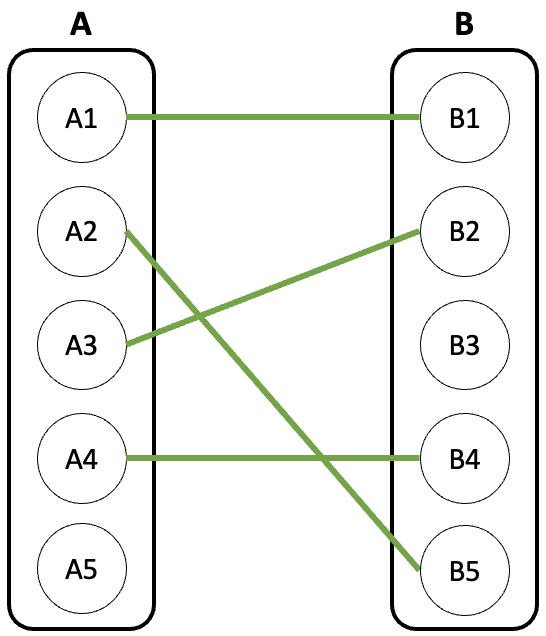
최종 매칭된 그래프는 아래와 같다.

최종 이분 매칭 그래프 모습

코드

int n, m;
vector<int> jobs[1001];
int assign[1001]; // assign[i] = B그룹의 i번 노드가 누구에게 매칭됨?
bool done[1001]; // done[i] = 진행 중인 DFS에서 B그룹의 i번 노드를 고려한 적이 있는가?

bool dfs(int x) {
    for (int i = 0; i < jobs[x].size(); i++) {
        int job = jobs[x][i];
        if (done[job]) continue;
        done[job] = true;
        if (assign[job] == 0 || dfs(assign[job])) {
          // 아직 매칭이 안된 노드거나, 매칭을 변경해서 비울 수 있거나
            assign[job] = x;
            return true;
        }
    }
    return false;
}

int match() {
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
          fill(done, done + 1001, false);
          if (dfs(i)) ans += 1;
    }
    return ans;
}

여러 블로그 포스터를 보면 구현 코드가 약간씩 다르다.
그 차이는 done[]의 정의이다.
만약 A 그룹을 기준으로 고려 여부를 확인하고 싶다면, for문 밖에서 확인해야 한다.
위 코드는 B그룹을 기준으로 확인하는 경우이다.

fill(done, done + 1001, false);을 개선하여 시간을 단축하는 방법이 있다. 이는 여기를 참고하자.