모스 알고리즘(Mo's algorithm)
개요
모스 알고리즘은 업데이트가 없는 구간 쿼리들을 빠르게 처리하는 알고리즘이다. 이때 쿼리는 구간의 합, 최댓값, 최솟값 등이 될 수 있다.
기본 아이디어는 아주 간단하다. ‘앞선 쿼리로 인해 계산된 값을 최대한 활용하자‘이다.
특히 쿼리의 순서를 자유롭게 바꿀 수 있는 환경(즉, 조회만 하는 경우)에는 앞선 쿼리에서 많은 정보를 다시 이용할 수 있을 것이다.
모스 알고리즘은 2가지의 알고리즘이 함께 이용된다.
- 오프라인 쿼리(Offline Query) : 여러개의 쿼리가 들어왔을 때 순서대로 처리하지 말고, 계산하기 유리하도록 순서를 바꾸어 처리하자.
- 평방 분활(Sqrt Decomposition) : 원소들의 각 구간을 \(\sqrt{n}\)개로 분할하여 관리하자. 이때 각 구간의 원소 개수도 \(\sqrt{n}\)개 이다. (구간 개수*구간별 원소 개수 = n)
모스 알고리즘의 아이디어는 간단하지만, 이 알고리즘의 시간 복잡도에 대해서는 증명이 필요하다. 증명은 여기를 참고하자.
구현
쿼리를 입력받는다. 이때 쿼리는 [구간 시작, 구간 끝]으로 이루어져 있다고 하자. 그리고 이 쿼리는 배열의 insert, delete, update 없이 조회하는 기능만 있으므로, 순서를 자유롭게 재배치해도 된다.(오프라인 쿼리)
\([L_i, R_i]\) 형태의 쿼리들을 다음과 같은 우선순위에 따라 순서를 바꾸자.(배열 개수 $n$)
- \(\frac {L_i} {\sqrt{n}}\) 기준 오름차순 정렬 (여기서 \(\sqrt{n}\)으로 나누는게 Sqrt Decomposition)
- \(\frac {L_i} {\sqrt{n}}\)가 서로 같다면, \(R_i\) 기준 오름차순 정렬
그 다음에는 투포인트를 사용하는 것처럼 필요한 부분은 더 반영하고, 구간에서 빠져야 하는 부분은 제외시키면 된다.
예제
이 문제의 예제 입력을 모스 알고리즘을 이용하여 풀어보자.
해당 문제의 쿼리는 구간의 원소의 합이다. 각 쿼리의 구간은 [1, 3], [2, 4], [5, 5]이다.
우리는 배열 인덱스로 사용하기 위해 모든 인덱스에서 1을 감소시킨 [0, 2], [1, 3], [4, 4]을 사용하자.
먼저 쿼리를 sort를 이용해 정렬해주자. 이때 정답을 출력할 때는 순서를 유지해야하므로 쿼리 순서도 함께 저장했다.
참고로 아래 코드에서 get<0>는 tuple에서 0번째 원소를 꺼내는 역할을 한다.
1
2
3
4
5
6
7
8
9
10
for (int i = 0; i < q; ++i) {
cin >> a >> b;
query[i] = {a - 1, b - 1, i};
}
sqrtN = sqrt(n);
sort(query, query + q, [](tuple<int, int, int> &a, tuple<int, int, int> &b) {
int af = get<0>(a) / sqrtN, bf = get<0>(b) / sqrtN;
if (af == bf) return get<1>(a) < get<1>(b);
else return af < bf;
});
이제 투포인터처럼 left, right를 조절해가며 연산을 수행하면 된다.
이때 첫 쿼리는 구간을 linear하게 탐색하며 직접 구해야한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int idx, s, e, left, right, sum = 0;
tie(s, e, idx) = query[0];
for (int i = s; i <= e; ++i) {
sum += arr[i];
}
ans[idx] = sum;
left = s, right = e;
for (int i = 1; i < q; ++i) {
tie(s, e, idx) = query[i];
while (left > s) sum += arr[--left];
while (left < s) sum -= arr[left++];
while (right > e) sum -= arr[right--];
while (right < e) sum += arr[++right];
ans[idx] = sum;
}
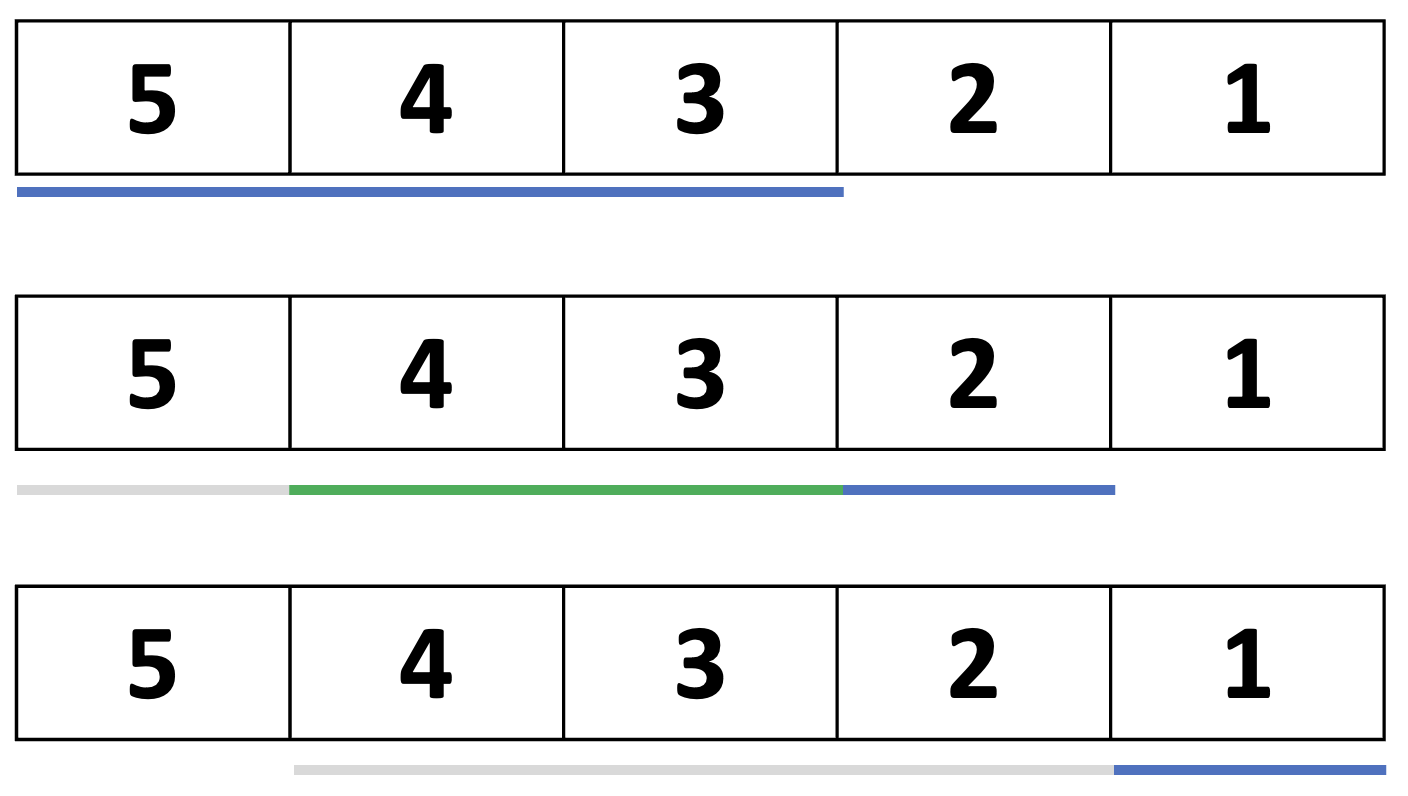
그림으로 표현하면 아래와 같다. 파란색 밑줄은 해당 쿼리에서 새롭게 반영한 부분, 초록색은 기존 정보를 재사용한 부분, 회색 부분은 제외시킨 부분이다.
문제 추천
함께 풀면 좋은 문제: https://www.acmicpc.net/problem/13547
평방 분활과 함께 사용하는 문제: https://www.acmicpc.net/problem/13546