느리게 갱신되는 세그먼트 트리
세그먼트 트리는 배열의 연속된 구간의 합, 최댓값, 최솟값 등을 구하는데 $O(\log N)$으로 처리할 수 있다. 특히 배열의 한 원소의 값이 변경됐을 때 $O(\log N)$으로 업데이트가 가능하다. 백준 기준 골드 상위권 티어부터 자주 사용되는 단골 알고리즘이다.
하지만 배열의 i번째 수부터 j번째 수에 v를 더하는 쿼리는 어떨까? (j-i+1)개의 원소 개수가 바뀌었으니, 세그 트리를 업데이트하는데 걸리는 시간은 $O(N \log N)$이다. 그냥 배열에서 구간 업데이트를 하면 $O(N)$인데, 이것보다도 더 느리다.
이때 사용하는 알고리즘은 ‘느리게 생신되는 세그먼트 트리(Segment Tree with Lazy Propagation)’이다. 핵심 아이디어는 아래와 같다.
업데이트 쿼리를 바로 적용하지 말고 임시로 저장만 해놨다가, 나중에 방문할 일이 생기면 그때 업데이트하자.
예시1
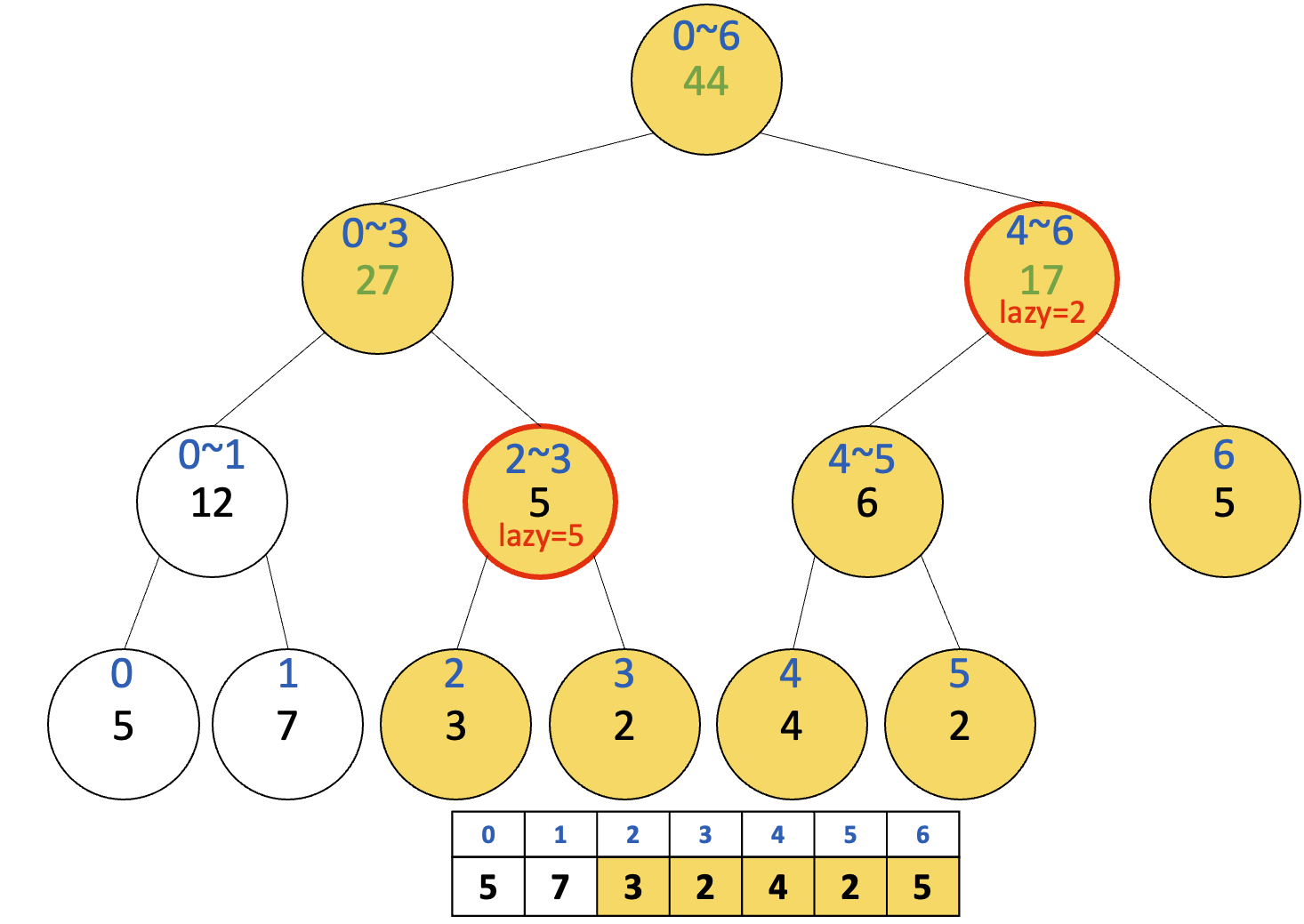
사용된 정수 배열은 [5, 4, 3, 2, 1, 2, 5] 이고, 각 구간의 합을 나타내는 세그먼트 트리는 아래 이미지와 같다. 노드마다 파란색으로 적혀있는 것은 해당 노드가 고려하는 배열의 구간을 뜻한다.(a~b는 구간 [a, b]이다.)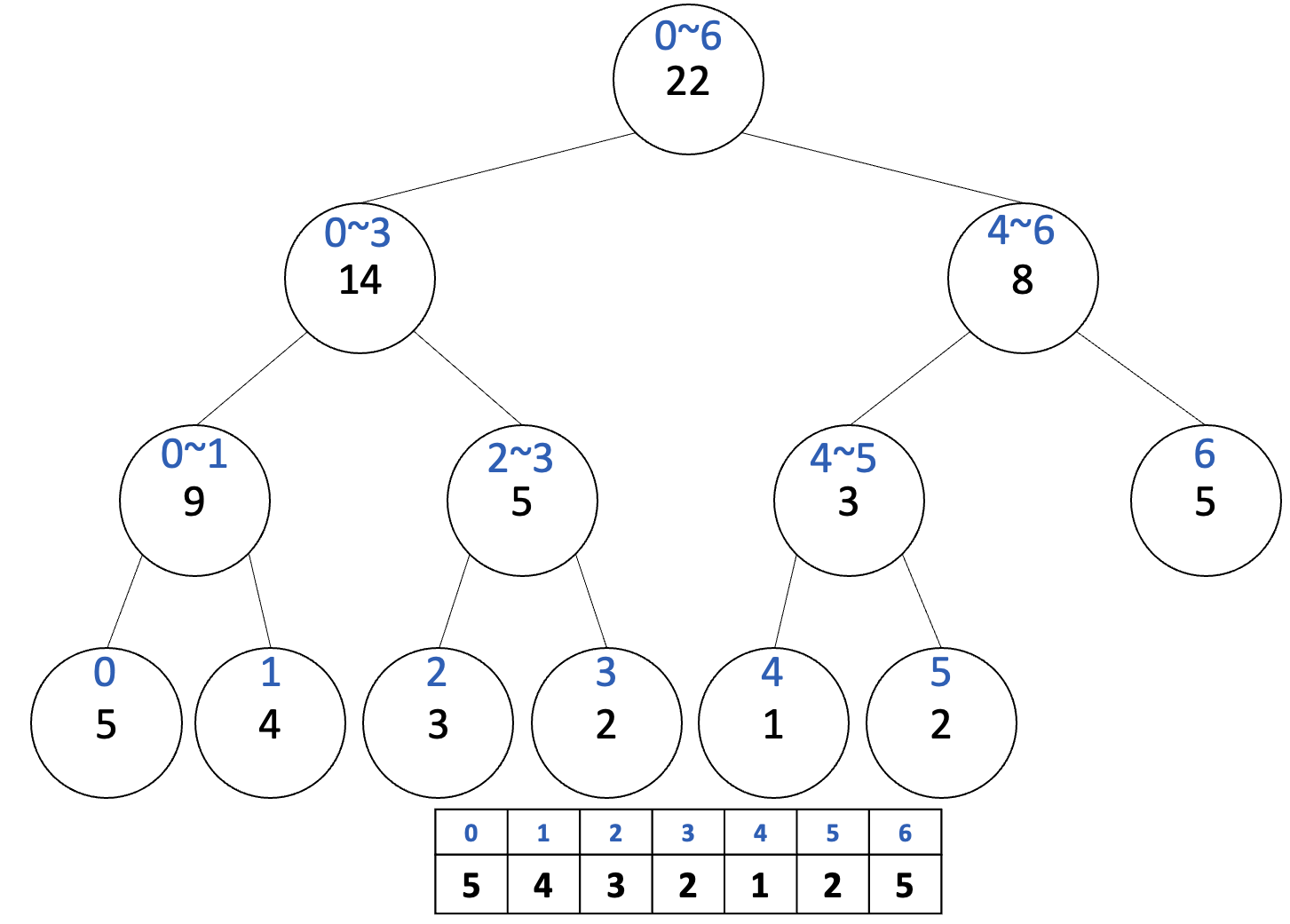 
업데이트 쿼리를 해보자. 구간 [1, 4]에 속하는 각 원소에 +3을 하고자 한다.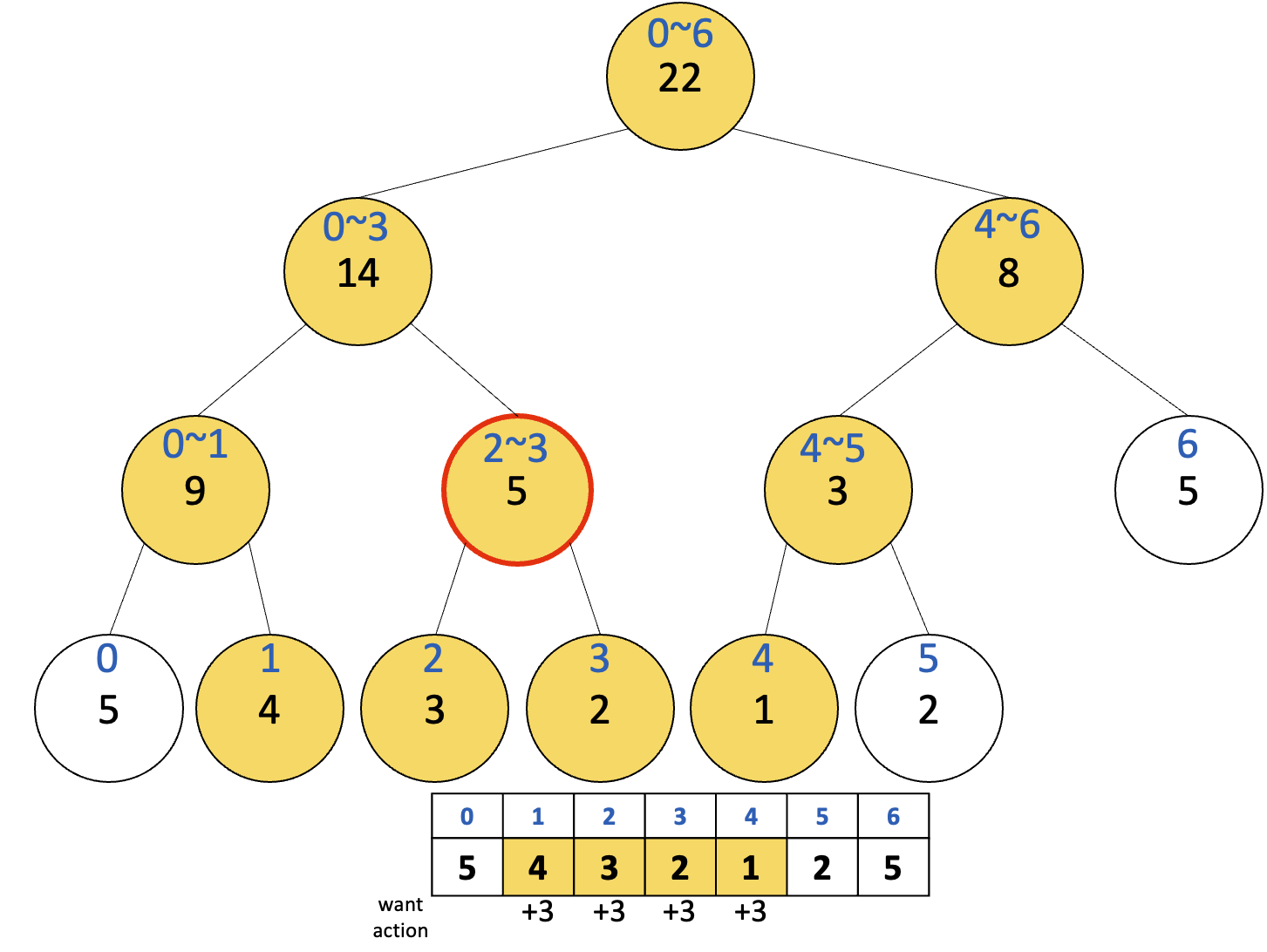 
노란색으로 칠해진 노드는 업데이트가 필요한 노드이다.(즉, 노드가 고려하는 구간 중에 1, 2, 3, 4가 하나라도 포함된 경우이다.)
이때 주목해야 하는 노드는 구간 [2, 3]을 담당하는 노드이다. 그 특징은 ‘그 노드를 루트로 하는 서브 트리의 모든 노드가 업데이트 되어야 한다.’ 이다.
여기서 사용하는 아이디어는 ‘그 하위 노드를 당장 업데이트 하지는 말자’ 이다. (제목에 있는 ‘느리게 갱신되는’이 이 아이디어를 의미한다.)
lazy[] 라는 배열을 사용하자. 이 배열에는 나중에 그 노드를 방문할 때 더할 값을 저장하자.
포스팅 뒷부분에 나올 코드를 통해 이를 어떻게 구현할지 살펴보자.
예시2
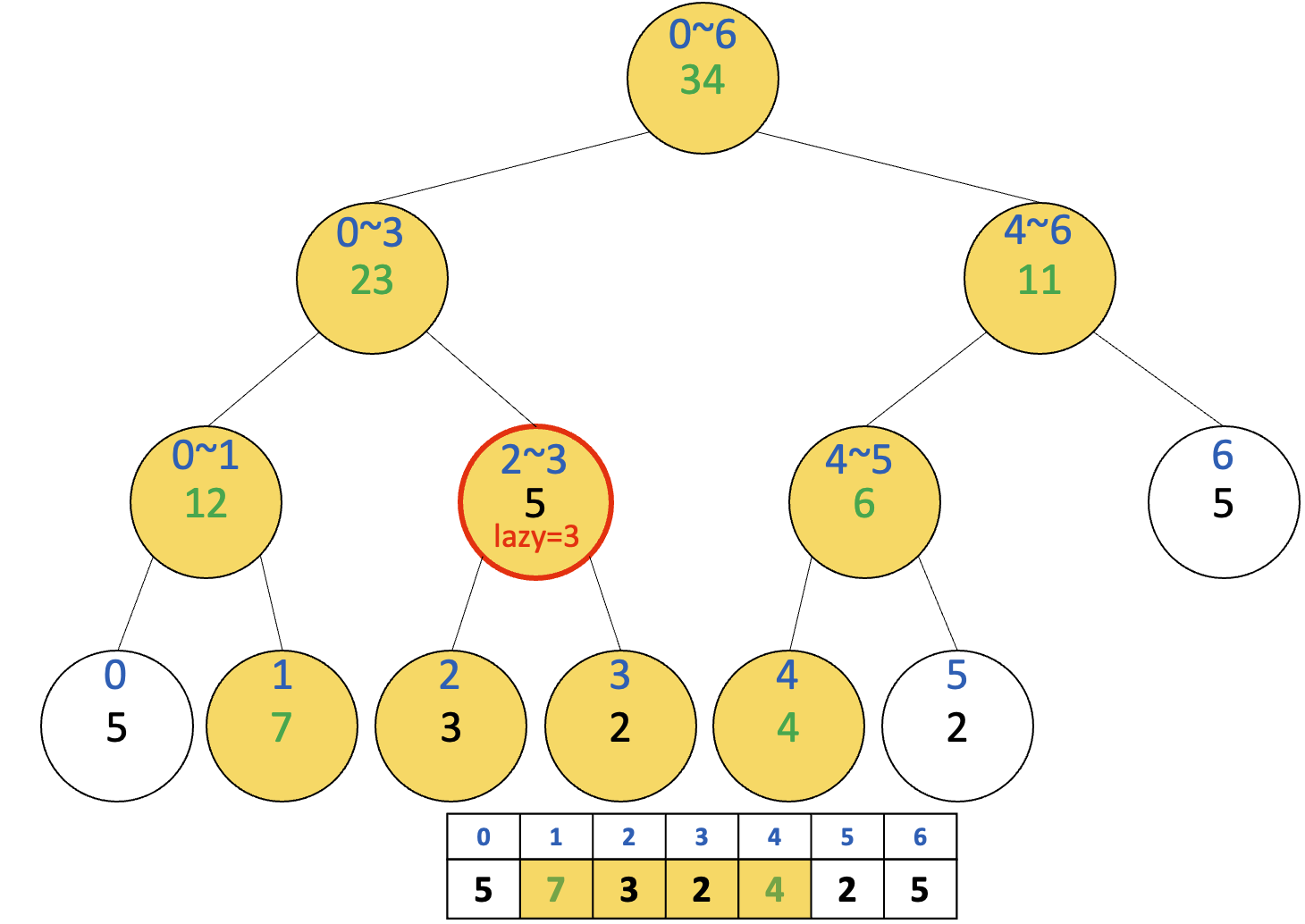
예시1에 이어서, 이번에는 구간 [2, 6]의 원소들을 각각 +2 할 것이다. 주목해야 하는 노드는 [2, 3]을 나타내는 노드와 [4, 6]을 나타내는 노드이다.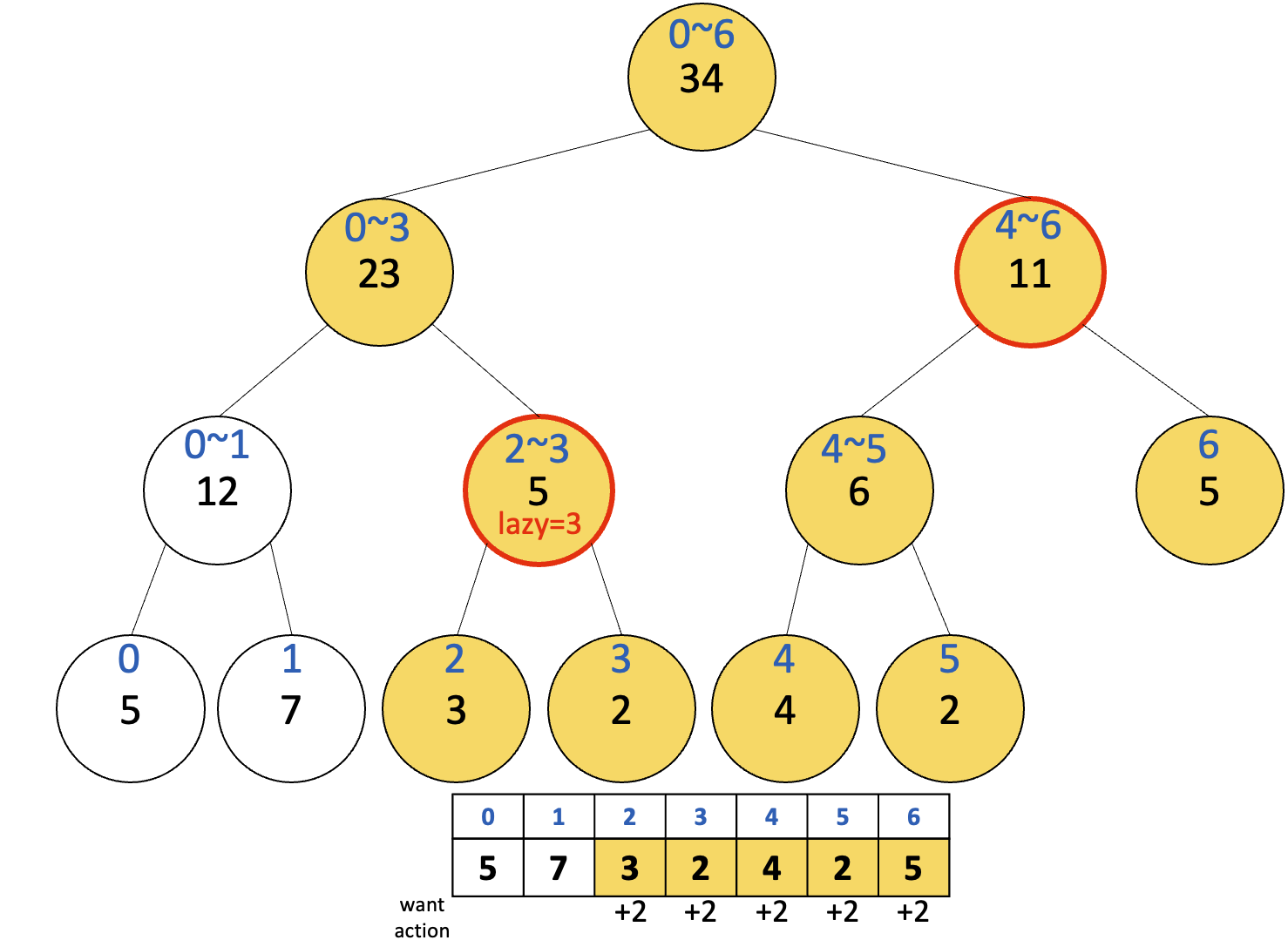 
마찬가지로 lazy 배열에 임시로 저장만 해놨다가, 나중에 방문할 때 업데이트 하면 된다.
이때 [2, 3] 노드에 예시1로 인해 존재하던 lazy=3이 lazy=5로 업데이트된 것을 확인하자.
코드
세그먼트 트리 코드를 기반으로 몇 가지 코드를 추가하면 된다.
1
2
3
4
5
6
7
8
9
void makeTree(int start, int end, int node) {
if (start == end) tree[node] = arr[start];
else {
int mid = (start + end) / 2;
makeTree(start, mid, node*2);
makeTree(mid + 1, end, node*2 + 1);
tree[node] = tree[node*2] + tree[node*2 + 1];
}
}
세그먼트 트리를 만드는 코드는 기존과 동일하다.
1
2
3
4
5
6
7
8
9
10
void updateLazy(int start, int end, int node) {
if (lazy[node] != 0) {
tree[node] += (end - start + 1) * lazy[node]; // leaf 노드 개수가 (end-start+1)개
if (start != end) {
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
}
업데이트 쿼리나 find 쿼리에서 사용할 함수이다.
lazy[node]!=0이라는 것은, 본인이 루트인 서브 트리의 모든 노드가 업데이트 되어야 한다는 이야기이다.
따라서 본인 노드에 값을 더하고, 자식들에게 전파(propagation)하면 된다.
이때 tree[node] += (end - start + 1) * lazy[node]인 이유는 구간에 속하는 leaf 노드 개수가 (end-start+1)이기 때문이다.
예를 들어, 구간 [2, 4]에 +3을 더하고자 한다면, 구간[2, 4]를 담당하는 노드는 +9를 해야한다.
1
2
3
4
5
6
7
8
9
int find(int left, int right, int start, int end, int node) {
updateLazy(start, end, node);
if (right < start || end < left) return 0;
else if (left <= start && end <= right) return tree[node];
else {
int mid = (start + end) / 2;
return find(left, right, start, mid, node * 2) + find(left, right, mid + 1, end, node * 2 + 1);
}
}
구간의 합을 구하는 함수이다. 기존과 크게 다르지 않지만, updateLazy()를 호출하는게 추가됐다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void updateRange(int left, int right, int start, int end, int node, long long diff) {
updateLazy(start, end, node);
if (right < start || end < left) return;
else if (left <= start && end <= right) {
tree[node] += (end - start + 1) * diff;
if (start != end) {
lazy[node * 2] += diff;
lazy[node * 2 + 1] += diff;
}
}
else {
int mid = (start + end) / 2;
updateRange(left, right, start, mid, node * 2, diff);
updateRange(left, right, mid + 1, end, node * 2 + 1, diff);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
특정 구간에 수를 더하는 함수이다.
현재 노드의 자식들이 모두 업데이트 대상이라면(즉, left <= start && end <= right) 더 이상 진행하지 않고, lazy에 값을 보관해두는게 포인트이다.